O caminhão ilustrado abaixo, está com sua lança esticada desde seu eixo até a sua ponta . Sua inclinação é de em relação à horizontal. A massa da lança é e para simplificar os cálculos considere-a uniformemente distribuída. O caminhão está estacionado, com a lança sustentando uma viga de aço de de comprimento e massa , que se encontra na posição horizontal. De forma a manter tudo em equilíbrio estático, um braço hidráulico no topo da cabine de controle, inclinado de em relação à horizontal, atua com uma força no centro de massa da lança . Despreze o atrito da lança com o eixo e as masas dos cabos e do gancho.
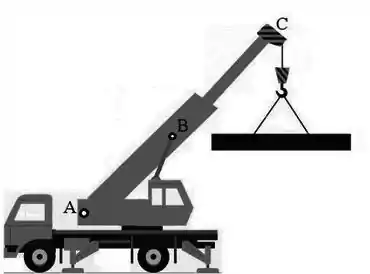
Utilize: ; ; ; .
Determine o vetor torque em relação ao eixo exercido pelo braço hidráulico sobre a lança.
Determine o vetor força que atua sobre a extremidade da lança presa ao eixo
Suponha agora que em determinado instante, o braço hidráulico pare de atuar, calcule para este instante o módulo da aceleração angular da lança.
Passo 1
Caraca...que enunciado longo! Mas não se assuste, se liga na resolução!
Para resolver o item , precisamos lembrar da fórmula de torque ou . Lembrou? Então, vamos lá, o que a gente precisa saber é a força exercida pelo braço, a distância de onde o braço atua até o eixo da lança e o ângulo entre esses dois vetores. Ahh...tranquilo!
Esse valor foi dado no enunciado
Epaa...de onde surgiu esse ? Bom, o enunciado disse que o centro de massa da lança se encontra em e que a massa da lança está uniformemente distribuída, e por causa disso, sabemos que , onde o braço hidráulico atua, é exatamente o meio da lança e portanto está à de distância do eixo ! Ahhh...agora sim!
Passo 2
Agora que já temos os dois valores, precisamos descobrir o ângulo entre eles. Mas isso não é muito difícil...olha só!
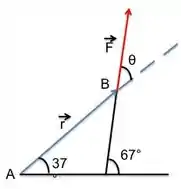
Achar agora ficou fácil!
Passo 3
Pronto! Agora podemos achar o torque. Lembrando que para descobrir o sentido e a direção do vetor torque, basta usar a regra da mão direita!
Passo 4
Vamos agora resolver o item . Para isso, temos que lembrar que no equilíbrio estático o somatório das forças e dos torques é nulo. Para achar a força , faremos o somatório para cada componente. Vamos começar pela componente .
Na componente , somente temos duas forças atuando, a componente da força no eixo , , e a componente da força que o braço hidráulico excerce em ,
Passo 5
Para a componente , temos, além das componentes das forças exercidas no eixo , , e no eixo , , a força peso da própria lança, e a força peso, da viga suspensa em .
Ou seja:
Passo 6
Vamos acabar logo com isso e resolver o item . Para calcular o módulo da aceleração angular no momento em que o braço hidráulico para de atuar, devemos lembrar que a aceleração em torno de um eixo é igual ao somatório dos torques dividido pelo momento de inércia em torno deste eixo.
Passo 7
Para achar o momento de Inérica, devemos lembrar do teorema dos eixos paralelos, , para a lança, temos:
Passo 8
Agora precisamos achar o torque! Podemos calcular o torque exatamente como fizemos para o item , no entanto agora estão atuando somente a força peso da lança e a força peso da viga.
Passo 9
Agora podemos calcular a aceleração angular:
Resposta