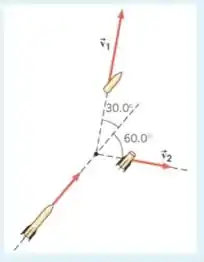
Um foguete de fogos de artifício de massa está se movendo a uma velocidade de magnitude . O foguete se divide em duas partes: um pedaço de massa voa com velocidade , e o segundo pedaço de massa voa com velocidade , como mostrado na figura. Se , qual é a magnitude de ?
Passo 1
Oi galera, tudo bem? Essa questão parece complicada, mas estou aqui para te ajudar! Vamos resolver juntos?
 Segura minha mão e vem comigo!
Segura minha mão e vem comigo!
Primeiro que esse desenho não tá lá essas coisas! Deixa eu fazer um aqui melhor pra ajudar na resolução!
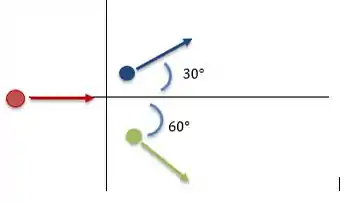
O momento inicial desse sistema é apenas o momento da bolinha vermelha. Essa bolinha tem massa e vai se dividir nas outras duas bolinhas: azul e verde. O problema diz que a bolinha azul tem massa , então a outra bolinha, a verde, também tem que ter a mesma massa, pois .
Daí as massas são:
A ideia aqui é usar a conservação de momento linear. Com base nesse desenho ver qual é o momento inicial e o final (que vai ser a soma dos momentos dos dois fragmentos depois da explosão) e igualar.
A gente sabe que o momento linear é uma grandeza vetorial, então a conservação tem que ser em cada direção.

Passo 2
Vamos agora identificar os vetores momento desse sistema.
Olhando de novo o esquema:
O momento inicial é dado pelo momento da bolinha vermelha, que tem velocidade e está na direção horizontal positiva. Então o momento é só em :
Agora o momento final tem duas componentes, dos fragmentos verde e azul. A componente do fragmento azul é e a componente é .
Já pro fragmento verde, temos que a componente é e a é .
Cada fragmento tem massa , e aí o vetor momento final é:
Tudo bem até aqui?
 Show!
Show!
Passo 3
Agora vamos usar o fato de que o momento é conservado! Então o momento inicial deve ser igual ao momento final:
 Calma! Ele é conservado componente a componente! Então vamos tirar daí duas equações com duas incógnitas =)
Calma! Ele é conservado componente a componente! Então vamos tirar daí duas equações com duas incógnitas =)
 Saca só:
Saca só:
Da equação pra temos:

E agora da equação pra podemos achar a velocidade :
Isso porque
Daí temos:

As velocidades dos fragmentos são:
O problema pediu só a magnitude de , mas se perguntar você já sabe!
Ufa! Terminamos!
Bora pra próxima?