Uma bomba centrífuga é instalada em um sistema de tubulações com comprimento e diâmetro , feitas de ferro fundido. A superfície do reservatório a jusante (após) a bomba está abaixo do reservatório a montante da bomba (antes). Determine a curva do sistema. Estime a potência necessária para que a bomba funcione à vazão de . Os reservatórios estão abertos para a atmosfera.
Passo 1
O enunciado descreve uma instalação e pede primeiro pra determinar a curva do sistema. Precisamos, então, lembrar quem é o , lá da teoria. Partindo do balanço de energia dividido por , é só isolar o e todo o resto é . O balanço de energia é:
Nesses casos de reservatórios, é conveniente usar a superfície dos reservatórios como esses pontos 1 e 2 a serem analisados. Chamando de:
E isso é conveniente porque o volume de líquido saindo ou entrando em um reservatório é muito pequeno face ao volume que tem nele. Aí podemos aproximar que altura de líquido quase não se move, daí:
Outro ponto importante sobre estes reservatórios é que estão abertos para a atmosfera e como escolhemos pontos na superfície do líquido, isto é, em contato com a atmosfera:
Substituindo isso tudo no balanço de energia:
Dividindo por e isolando o :
Podemos, ainda, abrir esse termo de perda de carga total:
Em que:
Como o enunciado não fala nada de acidentes (exemplo: válvulas, curvas etc), só tem esse termo . E podemos escrevê-lo em termos do fator de atrito de Moody :
Em que esse é a velocidade média dentro da tubulação.
Substituindo no balanço de energia:
![]()
Em que o termo em vermelho é o .
Substituindo os valores dados no enunciado
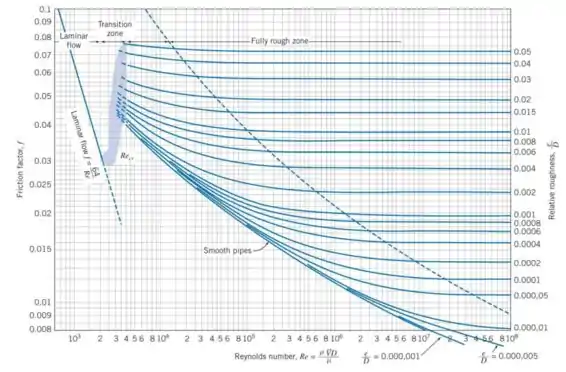
Como é função de , o valor de varia conforme a varia (ou ; dá no mesmo). Daí, vamos ter que estimar para cada vazão analisada; para isso, pode-se usar ou a correlação de Colebrook ou o diagrama de Moody. Vou usar a segunda opção.
Passo 2
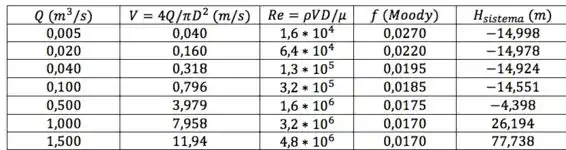
Para construir a curva do sistema, precisamos do valor de para diferentes valores de vazão . Vou construir uma tabela pra organizar a obtenção desses pontos, ok? E vou usar nos cálculos, para a água:
Também vamos precisar da rugosidade do ferro fundido para ver os valores no diagrama de Moody. Procurando na literatura:
Daí:
Aí, variando valores de vazão:
Plotando valores de , obtemos a curva do sistema:
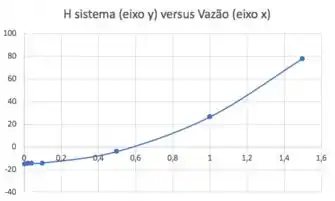
E quero destacar uma coisa pra você: esses pontos em que deu negativo significa que não precisaria de bomba nesses casos; só a diferença de altura já daria conta do transporte do líquido de um ponto a outro. Lembre que a definição de é quanto de carga o sistema precisa naquelas condições.
Passo 3
Por fim, é pedido pra calcular a potência da bomba que opere à vazão de .
“Ah, mas eu não lembro a fórmula de potência”! Então bora pelas unidades. Uma unidade de potência é . Temos que a unidade de está em . Daí, dá pra chegar em:
Alternativamente:
Agora é só lembrar que no ponto de operação:
E com nós já calculamos está na tabela. Daí: