Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução a Máquinas de Fluxo

Ver Teoria
Exercício 4123567

Enunciado

(Adaptada) Considere as dimensões do rotor da bomba centrífuga r 1 = 175   m m , r 2 = 500   m m , b 1 = 50   m m , b 2 = 30   m m , β 1 = 65 ° . Para um escoamento de água com entrada na bomba puramente axial, rotor a 750 rpm e vazão de 0,75 m³/s, estime a altura de carga e a potência mecânica de entrada ideais se o ângulo de saída da pá for (a) β 2 = 7 5 ° (b) β 2 = 85 ° (c) Compare os resultados.

Passo 1

Olá! 😊 Esse exercício é parecido com o anterior, pois tem a mesma geometria (os mesmos raios, mesmas larguras e mesmo ângulo de entrada). Além disso, queremos calcular de novo a altura de carga H e a potência W m ˙

“Tá ok. Mas o que essa questão tem de diferente?”

Duas coisas! A primeira é que vamos calcular a carga e potência para dois ângulos de saída diferentes e comparar os resultados. A segunda é que esse enunciado diz que a entrada é puramente axial. Logo, a velocidade tangencial de entrada é 0

V t 1 = 0

Então, vamos organizar nossos dados no Sistema Internacional e mãos à obra!

Raios: r 1 = 175   m m = 0,175   m e r 2 = 500   m m = 0,5   m  

Larguras: b 1 = 50   m m = 0,05   m e b 2 = 30   m m = 0,03   m

Ângulo: β 1 = 65 °   o u   1,13   r a d

Velocidade angular

ω = 750   r o t m i n 2 π   r a d 1   r o t 1   m i n 60   s = 78,5   r a d / s

Vazão: Q   =   0,75 m 3 / s

Além disso, fazendo a hipótese de fluido incompressível (água)

  m ˙ = ρ Q = 1000 × 0,75 = 750   m 3 / s

Passo 2

Para calcular   H t e ó r i c a e W ˙ m   , vamos precisar conhecer as velocidades U 1 ,   V t 1 , U 2 ,   V t 2

Para calcular U, vamos lembrar da física que V = ω . R . Então, fica assim:

U 1 = ω . r 1 = 78,5   × 0,175

U 2 = ω . r 2 = 78,5   × 0,5

Fazendo as contas, U 1 = 13,74   m / s e U 2 = 39,25   m / s

Além disso, pelo enunciado, a velocidade tangencial de entrada é nula pois a entrada é puramente axial

V t 1 = 0

Por outro lado, a saída não é puramente axial, então pela geometria conseguimos achar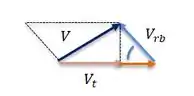 V t 2

U 2 = V t 2 + V r b 2 . c o s   β 2

Isolando V t 2

V t 2 = U 2 - V r b 2 . c o s   β 2

U 2 é conhecido, mas falta encontrar V r b 2 . Pela definição de vazão e continuidade

Q = V . A

Aplicando no caso da saída da bomba

Q = 2 π . R 2 . b 2 V n 2 = 2 π . R 2 . b 2 V n 2 . s e n     β 2

Isolando V r b 2

V r b 2 = Q 2 π . R 2 . b 2 . s e n     β 2  

Substituindo

V t 2 = U 2 - Q 2 π . R 2 . b 2 . s e n     β 2   c o s   β 2

V t 2 = U 2 - Q 2 π . R 2 . b 2   c o t   β 2

É nesse equação que queria chegar. Na letra a, o exercício diz que β 2 = 75 ° , logo

V t 2 = 39,25 - 0,75 2 π . 0,5.0,03 . c o t   7 5 °

V t 2 = 3 7 , 12   m / s

Assim, conseguiremos calcular   H t e ó r i c a e W ˙ m para β 2 = 75 °

H t e ó r i c a =   U 2 V t 2 - U 1 V t 1 g

Substituindo o que encontramos até agora 😊

H t e ó r i c a =   39,25 × 37,12   - 13,74 × 0 9,8

H t e ó r i c a =   148,7   m

Além disso, a potência mecânica de entrada ideal é

W ˙ m =   U 2 V t 2 - U 1 V t 1   m ˙

Substituindo

W ˙ m =   39,25 × 37,12   - 13,74 × 0 × 750

W ˙ m = 1,09 × 10 6 W

Com isso, nós encontramos a resposta da letra a. Para ângulo de saída da bomba β 2 = 75 ° , H t e ó r i c a =   148,7   m e W ˙ m = 1,09 × 10 6 W

Passo 3

Vamos fazer juntos a mesma estratégia para β 2 = 85 ° ? Eu ouvi um “Siiiim!”? hahaha

As velocidades U 1 e U 2 são as mesmas porque dependem só dos raios e velocidade do rotor que não mudaram. Além disso, V t 1 continua sendo zero, pois a entrada é só axial.

Falta então recalcular V t 2 . Vamos resgatar a equação que calcula ela (desenvolvemos no passo anterior)

V t 2 = U 2 - Q 2 π . R 2 . b 2 cot ⁡ β 2

Com β 2 = 85 ° agora

V t 2 = 39,25 - 0,75 2 π . 0,5.0,03 . c o t   8 5 °

V t 2 = 3 8,55   m / s

Com o V t 2 atualizado, vamos calcular a altura de carga

H t e ó r i c a =   U 2 V t 2 - U 1 V t 1 g

H t e ó r i c a =   39,25 × 3 8,55   - 13,74 × 0 9,8

H t e ó r i c a =   1 54,4   m

E então, a potência mecânica de entrada ideal é

W ˙ m =   U 2 V t 2 - U 1 V t 1   m ˙

W ˙ m =   39,25 × 38,55   - 13,74 × 0 × 750

W ˙ m = 1 , 13 × 10 6 W

Assim, temos a resposta da letra b. Para ângulo de saída da bomba β 2 = 8 5 ° , H t e ó r i c a =   154,4   m e W ˙ m = 1 , 13 × 10 6 W

Passo 4

Comparando as respostas das letras a e b, temos o seguinte

(a) Para β 2 = 75 ° , H t e ó r i c a =   148,7   m e W ˙ m = 1,09 × 10 6 W

(b) Para β 2 = 85 ° , H t e ó r i c a =   154,4   m e W ˙ m = 1,13 × 10 6 W

Ou seja, para um ângulo β maior na saída, a altura de carga fornecida pela bomba é maior, assim como sua potência. :D

Resposta

(a) Para β 2 = 75 ° , H t e ó r i c a =   148,7   m e W ˙ m = 1,09 × 10 6 W

(b) Para β 2 = 85 ° , H t e ó r i c a =   154,4   m e W ˙ m = 1,13 × 10 6 W

(c) A altura de carga da bomba e a potência são maiores para β 2 = 85 ° em relação aos valores encontrados para β 2 = 7 5 °

Exercícios de Livros Relacionados

Vimos muitos exemplos no Capítulo 7 sobre a substituição de fluidos de trabalho, visando facilitar alcançar a similaridade entre modelos e protótipos. Descreva os efeitos de testes em um compressor us
Para o rotor do Problema 10.1, operando a 750 rpm, determine a vazão volumétrica para a qual a componente tangencial da velocidade de entrada é zero. Calcule a altura de carga teórica e a potência mec
Uma turbina de impulsão deve desenvolver 15 MW com roda única, em um local onde a altura de carga líquida é 350 m. Determine a velocidade, o diâmetro do rotor e o diâmetro do jato apropriado para oper
O Apêndice D contém mapas para a seleção de modelos de bombas e curvas de desempenho para modelos individuais de bombas. Use esses dados e as regras de similaridade para prever o desempenho e traçar c
Um modelo de bomba de água centrífuga, em escala 1 : 3 , produz uma vazão Q m = 1m 3 / s , com uma altura de carga H m = 5,4m , operando a N m = 5100r p m . Considerando eficiências comparáveis para m