As dimensões do rotor de uma bomba centrífuga são

A bomba é acionada a 1250 rpm para bombear água. Calcule a altura de carga teórica e a potência mecânica de alimentação da bomba, se a vazão for 340 m³/h.
Dados: e
Passo 1
O enunciado está pedindo 2 coisas: a altura de carga teórica () e a potência mecânica de alimentação da bomba (). Sabemos que elas estão relacionadas pela própria definição da carga:
Então, precisamos encontrar primeiro a potência () e a vazão mássica () para gente conseguir calcular a carga teórica (). Então bora lá!
Vamos começar com a vazão mássica, já que a vazão volumétrica () já foi dada no enunciado. Mas antes, bora converter as unidades para o S.I.:
Beleza! Pela definição de vazão mássica então:
Passo 2
Agora a gente precisa determinar o valor da potência (), porque foi pedido no enunciado, mas porque ele é necessário para calcularmos a altura de carga teórica ().
Pela equação de Euler, temos que a potência pode ser calculada por:
Em que as componentes da velocidade são ilustradas abaixo:
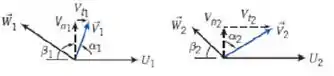
A única informação relativa à velocidade que foi informada é a da velocidade angular do sistema () e a gente pode relacionar ela com a velocidade da seguinte forma:
Como a velocidade angular () e os raios são conhecidos, podemos calcular e . Mas, antes, bora converter as unidades para o S.I.:
Com isso, para a seção :
E, para a seção :
Agora, só precisamos encontrar os valores das velocidades e para determinar a potência!
Passo 3
Bora encontrar as componentes tangenciais então! Para isso, dá uma olhadinha no sistema de vetores mais uma vez:
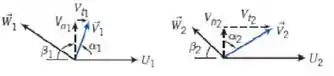
A gente pode ver que, tanto para a seção , quanto para a seção :
Então, reescrevendo em termos do que a gente quer () fica:
Pela definição da vazão volumétrica (), temos:
Vamos fazer para a seção 1, porque dá no mesmo depois fazer para a seção 2:
Podemos escrever a componente normal do vetor como sendo:
Substituindo:
Isolando a componente :
Pronto, agora a gente já tem uma expressão para e podemos substituir na expressão de para a seção :
Substituindo as informações do enunciado e as que já calculamos:
Fazendo a mesma sequência de passos, chegamos a uma equação para a seção :
Com os valores informados:
Passo 4
Agora calcular a potência ficou fácil:
Passo 5
E a carga é pode ser obtida da seguinte maneira: