Uma bomba centrífuga é utilizada para bombear 0,009 m³/s de água. A água entra no rotor axialmente através de um orifício de 32 mm de diâmetro. A velocidade de entrada é axial e uniforme. O diâmetro de saída do rotor é 100 mm. O escoamento sai do rotor a 3 m/s em relação às Pás, que são radiais na saída. A velocidade do rotor é 3450 rpm. Determine a largura de saída do rotor, , o torque de entrada e a potência requerida prevista pela equação de Euler para turbinas.
Passo 1
Beleza! Bora começar os trabalhos! O problema fala de uma bomba centrífuga usada pra bombear água, isso acontece como mostra essa imagem aqui em baixo:
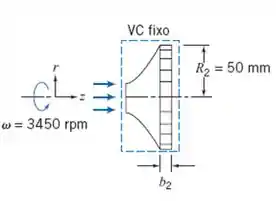
A água vem por uma tubulação e chega até a o “olho da bomba”. De lá o fluido é rotacionado e ganha energia de pressão, desempenhando então a função da bomba! ^^
Pra entender melhor como é o caminho completo da água pelo sistema, olha aqui as vistas frontal e lateral da bomba:
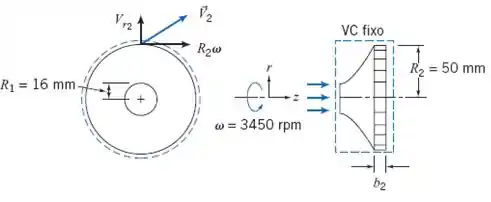
Essa parte mais a esquerda é como vemos a bomba de frente e na parte da direita é o que já vimos no começo: sua lateral.
Temos que achar agora três coisas:
- A largura de saída do rotor ()
- O torque de entrada ()
- A potência requerida ()
Então, bora resolver essa parada!
Passo 2
Pelo balanço material, a gente sabe que a vazão mássica () é dada por:
Já a vazão volumétrica () pode ser escrita como:
Em que é a área lateral da superfície cilíndrica e se refere a componente da velocidade perpendicular à .
A vazão de fluido que passa pela superfície ou pela é a mesma, mas como queremos achar a largura de saída do rotor (), vamos avaliar a equação para a superfície :
Esse representa a componente da velocidade que é normal à superfície .
Como queremos determinar a largura () e já conhecemos a vazão (), temos que:
Passo 3
Agora nosso objetivo será determinar o torque de eixo e a gente já viu que, para tratar de turbomáquinas, a equação de conservação da quantidade de movimento angular se resume à equação de Euler depois de todas as nossas suposições:
- Torque das forças de atrito e pressão desprezíveis
- Escoamento permanente e incompressível
- Escoamento uniforme (velocidades constantes) na entrada e na saída
- Campo gravitacional cancelado devido à simetria do volume de controle
Assim, ficamos com a equação de Euler:
Aplicando para o nosso volume de controle, teremos:
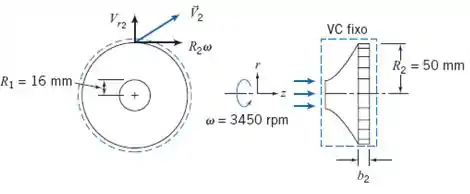
Como o fluido está entrando na direção do eixo do rotor, a velocidade tangencial na região onde é nula () e podemos reescrever a velocidades angular em função da velocidade de rotação :
Sendo assim, ficamos com:
Com a definição de vazão mássica (), temos que:
Antes de utilizar o valor da velocidade de rotação, temos que converter para as unidades S.I.:
Substituindo todos os valores informados e calculados na expressão do torque, temos que:
Passo 4
Agora que sabemos o valor do torque, fica fácil calcular a potência requerida (), basta usar a definição:
Substituindo as informações que temos: