Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução a Máquinas de Fluxo

Ver Teoria
Exercício 3124567

Enunciado

(Adaptada) Para o rotor da bomba centrífuga de dimensões r 1 = 75   m m , r 2 = 25 0   m m , b 1 = 38   m m , b 2 = 3 0   m m , β 1 = 6 0 ° e β 2 = 70 ° determine a velocidade de rotação para a qual a componente tangencial da velocidade de entrada é zero, se a vazão volumétrica for 910 m³/h. Calcule a altura de carga teórica e a potência mecânica teórica de entrada.

Passo 1

Para entender melhor esse exercício, vamos organizar esses dados aí? Temos

Raios: r 1 = 75   m m = 0,075   m e r 2 = 250   m m = 0,25   m  

Larguras: b 1 = 38   m m = 0,038   m e b 2 = 30   m m = 0,03   m

Ângulos: β 1 = 6 0 ° e β 2 = 70 °

O enunciado diz “a componente tangencial da velocidade de entrada é zero”, logo

V t 1 = 0

Vazão volumétrica

  Q   =   910   m 3 h 1 h 3600 s = 0,253 m 3 / s

Além disso, como o fluido é a água, ou seja, Podemos considerar incompressível

  m ˙ = ρ Q = 1000 × 0 , 253 = 253   m 3 / s

Pede-se a velocidade de rotação ω , a altura de carga teórica H t e ó r i c a e potência teórica W ˙ m

Passo 2

A velocidade de rotação pode ser calculada através de U, pois U = ω . R . Precisamos então usar alguma equação que envolva U para assim encontrar ω

Para isso, vamos utilizar definição de vazão e continuidade

Q = V . A

Visualizando a geometria da entrada da bomba e aplicando a equação da vazão

Q = 2 π . R 1 . b 1 . V n 1

Q = 2 π . R 1 . b 1 V r b 1 . s e n     β 1

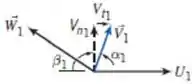
Com isso, rearrumando

V r b 1 = Q 2 π . R 1 . b 1 . s e n     β 1

Pela geometria

U 1 = V t 1 + V r b 1 . c o s   β 1

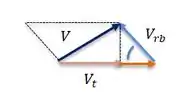
Isolando V t 1

V t 1 = U 1 - V r b 1 . c o s   β 1

Agora sim, conhecemos os termos e podemos substituir

0 = ω . R 1 - Q 2 π . R 1 . b 1 . s e n     β 1 . c o s   β 1

ω . R 1 = Q 2 π . R 1 . b 1 . c o t   β 1

ω = Q 2 π . R 1 2 . b 1 . c o t   β 1

Finalmente, substituindo os valores

ω = 0,253 2 π . 0,075 2 . 0,038 . c o t   6 0 °

ω = 108   r a d / s

Encontramos a velocidade de rotação!

Passo 3

Para calcular   H t e ó r i c a e W ˙ m   , precisamos saber quem são as velocidades U 1 ,   V t 1 , U 2 ,   V t 2

Como vimos no passo anterior, U = ω . R . Agora que conhecemos a velocidade de rotação, podemos calcular a velocidade U

U 1 = ω . r 1 = 108     × 0 , 0 75

U 2 = ω . r 2 = 108   × 0 , 2 5

Fazendo as contas, U 1 = 8,1   m / s e U 2 = 2 7   m / s

Além disso, pela geometria

U 2 = V t 2 + V r b 2 . c o s   β 2

Isolando V t 2

V t 2 = U 2 - V r b 2 . c o s   β 2

Acabamos de calcular U 2 . Mas quanto é V r b 2 ? De forma análoga a V r b 1 (calculado no passo anterior)

V r b 2 = Q 2 π . R 2 . b 2 . s e n     β 2  

Substituindo

V t 2 = U 2 - Q 2 π . R 2 . b 2 . s e n     β 2   c o s   β 2

V t 2 = U 2 - Q 2 π . R 2 . b 2   c o t   β 2

Substituindo agora os valores numéricos

V t 2 = 27 - 0 , 253 2 π . 0 , 2 5.0,03 . c o t   75 °

V t 2 = 25,56   m / s

Agora temos todos os valores para calcular a altura de carga teórica da bomba

H t e ó r i c a =   U 2 V t 2 - U 1 V t 1 g

H t e ó r i c a =   27 × 25,56   - 8,1 × 0 9,8

H t e ó r i c a =   70,4   m

Passo 4

Por fim, a potência mecânica teórica de entrada é

W ˙ m =   U 2 V t 2 - U 1 V t 1   m ˙

W ˙ m =   27 × 25,56   - 8,1 × 0 × 253

W ˙ m = 1 , 75 × 10 5 W

Resposta

ω = 108   r a d / s

H t e ó r i c a =   70,4   m

W ˙ m = 1,75 × 10 5 W

Exercícios de Livros Relacionados

Vimos muitos exemplos no Capítulo 7 sobre a substituição de fluidos de trabalho, visando facilitar alcançar a similaridade entre modelos e protótipos. Descreva os efeitos de testes em um compressor us
Para o rotor do Problema 10.1, operando a 750 rpm, determine a vazão volumétrica para a qual a componente tangencial da velocidade de entrada é zero. Calcule a altura de carga teórica e a potência mec
Uma turbina de impulsão deve desenvolver 15 MW com roda única, em um local onde a altura de carga líquida é 350 m. Determine a velocidade, o diâmetro do rotor e o diâmetro do jato apropriado para oper
O Apêndice D contém mapas para a seleção de modelos de bombas e curvas de desempenho para modelos individuais de bombas. Use esses dados e as regras de similaridade para prever o desempenho e traçar c
Um modelo de bomba de água centrífuga, em escala 1 : 3 , produz uma vazão Q m = 1m 3 / s , com uma altura de carga H m = 5,4m , operando a N m = 5100r p m . Considerando eficiências comparáveis para m