Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução a Máquinas de Fluxo

Ver Teoria
Exercício 1234567

Enunciado

As dimensões do rotor de uma bomba centrífuga são

A bomba trabalha com água e é acionada a 750 rpm. Calcule a altura de carga teórica e a potência mecânica de alimentação da bomba, se a vazão for 0,75 m³/s

Passo 1

Faaaala! Esse exercício nos deu já os raios r 1 e r 2 , as larguras b 1 e b 2 , os ângulos β 1 e β 2 , a velocidade angular da bomba e a vazão. Ufa! Bastante coisa

Anotando esses dados para deixar bem organizadinho, do jeito que os profs gostam. Já convertendo para o Sistema Internacional 😉

Raios

r 1 = 175   m m = 0,175   m

r 2 = 500   m m = 0,5   m  

Larguras

b 1 = 50   m m = 0,05   m

b 2 = 30   m m = 0,03   m

Ângulos

β 1 = 65 ° 2 π   r a d 360 ° = 1,13   r a d

β 2 = 70 ° 2 π   r a d 360 ° = 1,22   r a d

Velocidade angular

ω = 750   r o t m i n 2 π   r a d 1   r o t 1   m i n 60   s = 78,5   r a d / s

Vazão

Q   =   0,75 m 3 / s

E o que queremos? A altura de carga teórica, ou seja,   H t e ó r i c a e a potência mecânica de alimentação da bomba, isto é: W ˙ m

Para calcular   H t e ó r i c a e W ˙ m   essas formulas que vimos na teoria vão nos ajudar

H t e ó r i c a =   U 2 V t 2 - U 1 V t 1 g

W ˙ m =   U 2 V t 2 - U 1 V t 1   m ˙

Relaxa, com os dados do enunciado vamos conseguir encontrar as componentes da velocidade U e Vt. Aliás é justamente isso que faremos juntos no próximo passo

Passo 2

Em física nós aprendemos que V = ω . R , certo? Vamos aplicar isso aqui também!

U 1 = ω . r 1 = 78,5   × 0 , 175

U 2 = ω . r 2 = 78,5   × 0,5

Fazendo as contas, U 1 = 13,74   m / s e U 2 = 39,25   m / s

Para encontrar as velocidades tangenciais Vt, vamos lembrar da geometria do processo:

U i = V t i + V r b i . c o s   β i

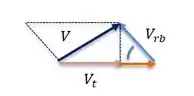
Isolando V t 1

V t i = U i - V r b i . c o s   β i

Beleza, U 1 a gente já conhece. Mas quem seria esse V r b 1 ? Pela definição de vazão

Q = V . A

E no nosso caso de bombas

Q = 2 π . R i . b i V n = 2 π . R i . b i . V r b i s e n     β 1

Isolando V r b i

V r b i = Q 2 π . R i . b i . s e n     β i  

Substituindo na equação da velocidade tangencial

V t i = U i - Q 2 π . R i . b i . s e n     β i . c o s   β i

Logo

V t i = U i - Q 2 π . R i . b i . c o t   β i

Agora sim, já conhecemos todo mundo 😊 Calculando a velocidade tangencial na entrada da bomba (1)

V t 1 = U 1 - Q 2 π . R 1 . b 1 . c o t   β 1

V t 1 = 13,74 - 0,75 2 π . 0,175 . 0,05 . c o t   65 °

V t 1 = 7,38   m / s

Para a saída da bomba (2), a velocidade tangencial é

V t 2 = U 2 - Q 2 π . R 2 . b 2 . c o t   β 2

V t 2 = 3 9 , 25 - 0,75 2 π . 0,5 . 0,03 . c o t   70 °

V t 2 = 3 6,35   m / s

Com isso, temos todos as variáveis que precisamos para o cálculo de   H t e ó r i c a e W ˙ m :D

Passo 3

A altura de carga teórica é

H t e ó r i c a =   U 2 V t 2 - U 1 V t 1 g

Substituindo os valores encontrados

H t e ó r i c a =   39,25 × 36,35   - 13,74 × 7,38 9,8

H t e ó r i c a =   135,2   m

Além disso, a potência mecânica de alimentação da bomba é

W ˙ m =   U 2 V t 2 - U 1 V t 1   m ˙

Como a água pode ser considerada um fluido incompressível

  m ˙ = ρ Q = 1000 × 0,75 = 750   m 3 / s

Substituindo os valores conhecidos

W ˙ m =   39,25 × 36,35   - 13,74 × 7,38 × 750

W ˙ m =   39,25 × 36,35   - 13,74 × 7,38 × 750

W ˙ m = 9,94 × 10 5 W

Encontramos a carga teórica e potência, como o exercício pediu 😉

Resposta

H t e ó r i c a = 135,2   m

W ˙ m = 9,94 × 10 5 W

Exercícios de Livros Relacionados

Vimos muitos exemplos no Capítulo 7 sobre a substituição de fluidos de trabalho, visando facilitar alcançar a similaridade entre modelos e protótipos. Descreva os efeitos de testes em um compressor us
Para o rotor do Problema 10.1, operando a 750 rpm, determine a vazão volumétrica para a qual a componente tangencial da velocidade de entrada é zero. Calcule a altura de carga teórica e a potência mec
Uma turbina de impulsão deve desenvolver 15 MW com roda única, em um local onde a altura de carga líquida é 350 m. Determine a velocidade, o diâmetro do rotor e o diâmetro do jato apropriado para oper
O Apêndice D contém mapas para a seleção de modelos de bombas e curvas de desempenho para modelos individuais de bombas. Use esses dados e as regras de similaridade para prever o desempenho e traçar c
Um modelo de bomba de água centrífuga, em escala 1 : 3 , produz uma vazão Q m = 1m 3 / s , com uma altura de carga H m = 5,4m , operando a N m = 5100r p m . Considerando eficiências comparáveis para m