Uma bomba centrífuga, girando a 3000 rpm, bombeia água a uma taxa de 0,6m³/min. A água entra axialmente, e deixa o rotor a 5,4 m/s relativo às pás, que são radiais na saída. Se a bomba requer 5 kW e tem eficiência de 72%, estime as dimensões básicas (diâmetro e largura de saída do rotor), usando a equação de Euler para as turbomáquinas.
Dados:
Passo 1
Esse problema é o que chamamos de projeto de equipamentos, pois vamos determinar as dimensões da bomba para atender certa condição de operação. Então, bora lá!
O sistema é muito parecido com o que a gente viu no exercício anterior:
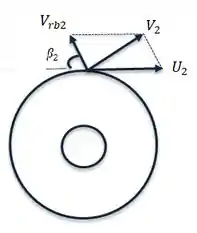
Como a entrada é axial, temos que a componente tangencial na região é nula:
Como o fluxo é radial na saída, para a região , podemos escrever que:
Podemos reescrever a componente em função da rotação do sistema:
Sendo assim:
Passo 2
Agora vamos olhar a potência.
A potência da turbomáquina () é dada por:
Logo:
A gente sabe que a vazão mássica () é dada por:
Convertendo a vazão volumétrica em unidades S.I.:
Nesse problema, temos pela primeira vez uma eficiência real, ou seja, estamos considerando aqui que o equipamento não é ideal. O equipamento “usa” uma potência de , mas só uma parte é efetivamente transferida para o sistema: 72%. Então, podemos escrever:
Pela equação que encontramos, podemos determinar o da seguinte maneira:
Antes de prosseguirmos, vamos converter a rotação em unidades S.I.:
Subsituindo agora os valores na expressão de :
E o diâmetro será duas vezes isso:
Passo 3
E pra calcular a largura da saída do rotor? Nosso querido ...
A gente pode escrever a componente normal () como sendo:
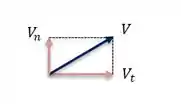
Observa que usamos o seno de 90° porque o fluxo de saída é radial.
Com isso, temos que: