Encontre a matriz transposta da matriz:
Passo 1
Vale lembrar que para obtermos a matriz transposta de uma matriz, basta pegarmos as linhas dessa matriz e transformá-las em colunas. Vamos ver um exemplo colorido:
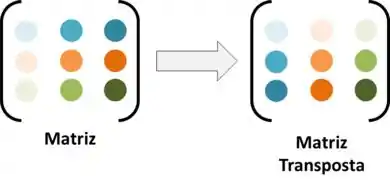
Repara que a primeira linha de bolinhas azul da matriz, virou a primeira coluna de bolinhas azul na matriz transposta. Repara também que a ordem das bolinhas não mudou, sempre indo da mais clara para mais escura.
Sendo assim, ao repetirmos essa ação fazemos com que as outras linhas da matriz formem as colunas da matriz transposta.
Então, o mesmo se repetiu para segunda linha de bolinhas laranjas, que virou a segunda coluna de bolinhas. E a terceira linha de bolinhas verdez, virou a terceira coluna de bolinhas verdes. Sempre da mais clara para mais escura.
Passo 2
Agora vamos fazer com a matriz do nosso problema:
Vamos começar transpondo a primeira linha, para primeira coluna.
Passamos para segunda linha, que virará a segunda coluna.
Por fim, vamos transpor a última linha, completando a nossa matriz transposta.