Sejam , e vetores do espaço tais que e são vetores unitários e ortogonais entre si e . Então o valor de
É igual a:
- 1
- -1
- 0
- 1/3
- -1/3
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou ajudar e resolver passo a passo com você! O problema nos deu três vetores:
e nos disse que . E perguntou qual é o valor de
Então a ideia é calcular quem é esse vetor , e calcular esse determinante e torcer para encontrarmos algo parecido.
Como os vetores e são unitários, o vetor também será, e podemos ter uma expressão para o módulo de , em termos das componentes de e , para comparar com o determinante dado.

Mas calma, vou fazer passo a passo com você!
Passo 2
Vamos começar calculando o vetor e seu módulo:
Beleza? E agora vamos calcular o módulo desse vetor:
Tranquilo até aqui?

Passo 3
Vamos calcular agora aquele determinante! O determinante é:
E substituindo as componentes de na última linha temos:
Agora bora calcular!

E agora com bastante atenção, vamos fazer essas multiplicações:

Então o valor do determinante encontrado foi:
Será que temos algo parecido já calculado?
Passo 4
Vamos comparar o módulo do vetor calculado no passo 2:
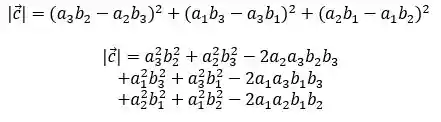
Com o valor do determinante que calculamos agora no passo 3:
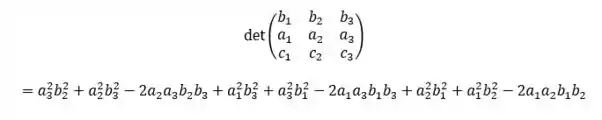
E vemos que o valor é o mesmo!

Como o vetor é o resultado do produto vetorial entre outros dois vetores unitários, ele tem módulo1! E como o determinante tem a mesma expressão que o módulo de , isso significa que o determinante vale 1!

Sendo assim, a resposta correta é (a). E é isso! Espero ter ajudado!