Indique os elementos da diagonal principal e os da diagonal secundária de cada uma das seguintes matrizes quadradas:
Passo 1
Primeiro, vamos lembrar o que é diagonal principal e secundária.
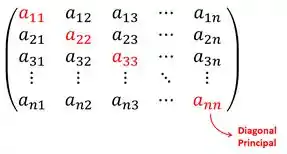

Passo 2
A nossa diagonal principal nesse caso vai ser:

Então os elementos da diagonal principal são :e
Agora a secundária :
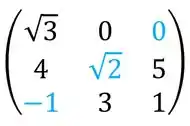
Assim, os elementos da diagonal secundária são :
e
Passo 3
Mesma ideia, nossa diagonal principal vai ser:
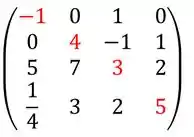
Assim , os elementos da diagonal principal são :
e
A secundária :

Assim, os elementos que temos na diagonal secundária são :e 0
Resposta
- Principal : e
- Principal: e
Secundária : e
Secundária: e