Sabendo que e , cacule a coordenada do vetor :
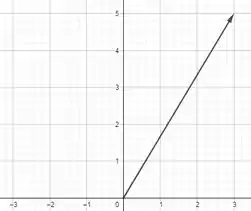
Passo 1
Lembrando que :
Para resolver isso, nós vamos pegar a coordenada de P e subtrair a coordenada O.
Para fazer essa subtração, é só diminuir valores de x com valores de x, e de y com de y :
Essa é a cordenada do sseu vetor.
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas de 7 a 11, determine se os elementos do conjunto de vetores dados são linearmente independentes. Se forem linearmente dependentes, encontre uma relação linear entre eles. Os v
Em cada um dos problemas de 7 a 11, determine se os elementos do conjunto de vetores dados são linearmente independentes. Se forem linearmente dependentes, encontre uma relação linear entre eles. Os v
Em cada um dos problemas de 1 a 6, resolva o sistema de equações dado ou mostre que não tem solução.1. x 1- x 3 = 0 3 x 1+ x 2 + x 3 = 1 - x 1 + x 2 + 2 x 3 = 2
Em cada um dos problemas de 7 a 11, determine se os elementos do conjunto de vetores dados são linearmente independentes. Se forem linearmente dependentes, encontre uma relação linear entre eles. Os v
Em cada um dos problemas de 7 a 11, determine se os elementos do conjunto de vetores dados são linearmente independentes. Se forem linearmente dependentes, encontre uma relação linear entre eles. Os v