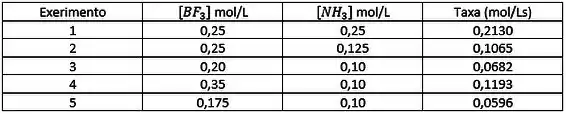
Para a seguinte reação em fase gasosa foram obtidos os seguintes valores de velocidade inicial em função da concentração inicial dos reagentes. Com base nestes resultados, determine a lei de velocidade desta reação, a ordem total e estime o valor da constante de velocidade.
Passo 1
A lei da velocidade da reação será algo como:
E o que precisamos fazer é determinar os valores de , e , a partir dos dados na tabela.
Passo 2
Começaremos usando dois experimentos onde a não seja alterada. Com constante, estudamos apenas o efeito da concentração de na velocidade.
Podemos usar os experimentos 3 e 4, 3 e 5 ou 4 e 5. Como entre 4 e 5 a concentração de cai pela metade, pode ser mais fácil estudar o efeito da alteração de na velocidade. Mas você pode escolher fazer com qualquer um dos três pares.
Agora dividimos por (ou o contrário). Dessa forma, vamos cortar as incógnitas e , e poderemos calcular .
Cortando o e o , que aparecem em cima e embaixo da fração e resolvendo a fração numérica:
Só mais um pouquinho de matemática:
Passo 3
Agora vamos usar as linhas 1 e 2, onde a concentração de é constante e a concentração de é alterada.
Agora dividimos por (ou o contrário). Dessa forma, vamos cortar as incógnitas e , e poderemos calcular .
Simplificando, nos resta:
Passo 4
Por enquanto, a nossa lei da velocidade está:
O que nos diz que a ordem global da reação é:
Passo 5
E, agora, vamos calcular o valor da constante.
Como alterações de concentração não mudam a constante, podemos usar qualquer um dos 5 experimentos para calcular o valor de .
E não podemos esquecer da unidade da constante:
Onde é a unidade da constante (e não a concentração!!!).
Resposta
Reação de segunda ordem global.
, onde