Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Ligações Iônicas

Ver Teoria
Exercício 101234567891112

Enunciado

Considere o composto hipotético C a F ( s ) .

a) Calcule a sua energia de rede. Suponha a estrutura do N a C l e uma distância internuclear de 2,67 . 10 - 10 m.

b) Faça o ciclo de Born-Haber para o C a F indicando todas as etapas.

c) Calcule a entalpia padrão de formação para o C a F , utilizando a resposta do item (a) e os dados termoquímicos que forem necessários.

Passo 1

Em primeiro lugar, bora destacar aquela palavrinha ali: hipotético! Sério, é só uma hipótese, tá? O composto iônico esperado entre cálcio e flúor é o C a F 2 e não C a F .

As informações aqui do passo 1, são dados que teriam que ser fornecidos pra você poder fazer essa questão, beleza?

Ali no item (a) ele te diz que a estrutura é semelhante à do N a C l pra você saber qual constante de Madelung usar. A constante de Madelung ( A ) pra estrutura do N a C l é A = 1,74756 .

No item (b), a gente só vai usar a 1ª energia de ionização do cálcio, porque esse cálcio aí do enunciado só vai perder um elétron (embora a gente saiba que o cálcio perde 2 elétrons e forma o C a 2 + , mas isso é um caso hipotético).

Pra fazer o item (c), na real, você precisa de muita informação.

  • Energia de sublimação do cálcio: ∆ H s u b l i m C a = 178,2 kJ/mol
  • Energia de dissociação do flúor: ∆ H d i s s o c F 2 = 157,9 kJ/mol
  • 1ª energia de ionização do cálcio: 1 ª E I = 590,0 kJ/mol
  • Afinidade eletrônica do flúor: A E   F = 328,0   kJ/mol

    • Pronto, bora calcular.

    Passo 2

    a) Pra calcular a energia de rede do C a F :

    U 0 = A N Z + Z - e 2 4 π ε 0 r 0 1 - 1 n

    A = c o n s t a n t e   d e   M a d e l u n g = 1,74756

    N = n ú m e r o   d e   a v o g r a d o = 6,02 . 10 23   m o l - 1

    Z + = c a r g a   d o   c á t i o n =   + 1       e       Z - = c a r g a   d o   â n i o n =   - 1

    e = c a r g a   d o   e l é t r o n = 1,602 . 10 - 19   C

    ε 0 = c o n s t a n t e   d e   p e r m i s s i v i d a d e   e l é t r i c a   d o   v á c u o = 8,85 . 10 - 12 C 2 / J m

    r 0 = d i s t â n c i a   i n t e r n u c l e a r   d a d o =   2,67 . 10 - 10   m

    Como cálcio assume a configuração do Ar e flúor assume a configuração do Ne:

    n = n A r + n N e 2 = 9 + 7 2 = 8

    Joga tudo na fórmula:

    U 0 = 1,74756.6,02 . 10 23 + 1 . - 1 . ( 1,602 . 10 - 19 ) ² 4 π . 8,85 . 10 - 12 . 2,67 . 10 - 10 1 - 1 8

    Joga tudo na calculadora:

    U 0 = - 795604,57   J / m o l = - 795,6   k J / m o l

    Passo 3

    b) Duas formas diferentes de representar o Ciclo de Born-Haber pro C a F :

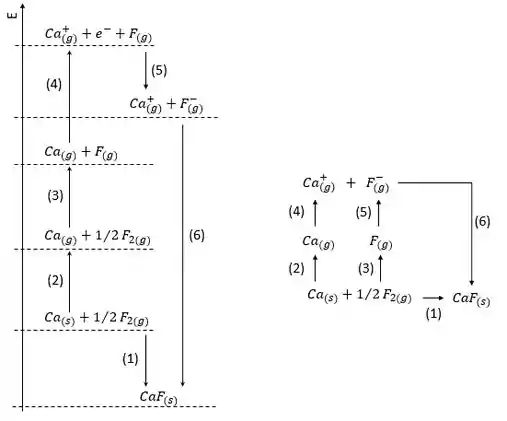
    Escolha a que você preferir. Ou melhor, a que o seu professor usa! :p

    E tem que dizer o que cada etapa aí representa:

    (1) Variação de entalpia de formação: ∆ H f ( C a F )

    (2) Energia de sublimação do cálcio: ∆ H s u b l i m   ( C a )

    (3) Energia de dissociação de meio mol de gás flúor: 1 2 ∆ H d i s s o c   ( F 2 )

    (4) 1ª Energia de ionização do cálcio: 1 ª   E I   ( C a )

    (5) Entalpia de ganho de elétrons: ∆ H g . e . ( F )

    (6) Energia do retículo cristalino ou energia de rede do C a F : U 0

    Passo 4

    c) Pra calcular a entalpia padrão de formação, a gente vai precisar saber todos aqueles dados do passo 1:

  • Energia de sublimação do cálcio: ∆ H s u b l i m C a = 178,2 kJ/mol
  • Energia de dissociação do flúor: ∆ H d i s s o c F 2 = 157,9 kJ/mol
  • 1ª energia de ionização do cálcio: 1 ª E I = 590,0 kJ/mol
  • Afinidade eletrônica do flúor: A E   F = 328,0   kJ/mol

Pelo ciclo de Born-Haber desenhado na esquerda, dá pra enxergar que:

5 +   6 =   1 +   2 +   3 +   4                 t o d o s   e m   m ó d u l o

Você pode preferir pensar que, partindo do C a s + 1 2 F 2 ( g ) e indo para o sólido iônico C a F ( s ) , a gente pode optar por dois caminhos. E como o caminho não interessa, a variação de energia pelos dois caminhos deve ser igual. “Um caminho deve ser igual ao outro”.

1 =   2 +   3 +   4 + 5 + 6       a t e n ç ã o   a o s   n e g a t i v o s   e   p o s i t i v o s                

O segundo jeito é melhor porque você já vai ver se a sua resposta tem que ser positiva ou negativa, valeu?

∆ H f C a F = ∆ H s u b l i m   C a + 1 2 ∆ H d i s s o c   F 2 + 1 ª   E I   C a + ∆ H g . e . + U 0

∆ H f C a F = ∆ H s u b l i m   C a + 1 2 ∆ H d i s s o c   F 2 + 1 ª   E I   C a - A E ( F ) + U 0

∆ H f C a F = 178,2 + 1 2 . 157,9 + 590,0 - 328,0 - 795,6

∆ H f C a F = -   276,45   k J / m o l

Resposta

a) U 0 = - 795,6   k J / m o l

c) ∆ H f C a F = -   276,45   k J / m o l

Exercícios de Livros Relacionados

A distância entre dois núcleos no equilíbrio da molécula de N a C l é 0,24 n m . Se a molécula é modelada como cargas + e e – e , separadas por 0,24 n m , qual é o momento de dipolo elétrico da molécu
Quando a molécula N a F faz uma transição de l = 3 até o nível rotacional de l = 2 , sem nenhuma variação no número quântico vibracional nem no estado eletrônico, um fóton de comprimento de onda igual
Uma molécula diatômica hipotética de oxigênio ( m a s s a = 2,656 × 10 - 26 k g ) e hidrogênio ( m a s s a = 1,67 × 10 - 27 k g ) emite um fóton de comprimento de onda 2,39 μ m quando efetua uma trans
A energia de ligação da molécula de cloreto de potássio ( K C l ) é igual a 4,43 e V . A energia de ionização de um átomo de potássio é igual a 4,3 e V e a afinidade eletrônica do cloro é de 3,6 e V .
Para a molécula do cloreto de sódio discutida no início da seção 42.1 qual é a distância máxima entre os íons para que haja estabilidade se eles forem considerados partículas puntiformes? Ou seja, qua