Observe o gráfico abaixo com o perfil energético de uma ligação iônica em função da distância entre os íons.
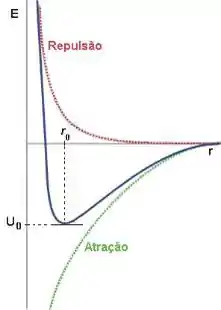
Explique a relação das curvas verde, vermelha e azul com os valores de , o significado de e .
Passo 1
Beleza, vamos começar falando da atração. Olhando só pra curva verde.
A ligação iônica é de origem eletrostática. Ou seja, os caras ficam ligados porque cargas positivas atraem as cargas negativas, e vice-versa (o famoso “os opostos de atraem”).
Quando o raio , que é a distância entre os núcleos dos átomos, fica muito grande, a atração é muito pequena, e a curva verde tende a zero.
Quando o raio é pequeno, os átomos estão próximo e a atração é grande. Quanto maior a atração, mais negativa é a energia (ela cresce em módulo).
Isso é explicado pela Lei de Coulomb. Por essa lei, a energia de atração entre o cátion e o ânion é dada por:
Olha aquele ali embaixo. Fica bem claro que, quando vai pro infinito, vai pra zero. E para muito pequenos, vai pro infinito em módulo. Como essa energia é negativa, ela vai para “menos infinito” ().
Ah, também fica claro que, quanto maior a carga dos íons, maior é a atração entre eles (mais negativa é ).
Passo 2
Agora vamos pensar na repulsão, a curvinha vermelha.
Beleza, a gente sabe que o cátion e o ânion vão se atrair de uma forma global. Mas todos eles tem elétrons, né? Então pensa nesses caras se aproximando, aproximando, aproximando...
Chega uma hora, que a eletrosfera de um enconta na eletrosfera do outro. Elétron tocando em elétron, uma confusão, gritaria.. Ruim né? Elétron não gosta de elétron! Cargas semelhantes se repelem.
Por isso aquele curva vermelha funciona assim: pra grande, sem problemas! Uma elestrosfera bem longe da outra, ninguém repele ninguém e a energia de repulsão tende a zero. Porém, pra distâncias muito pequenas, a repulsão é grande, e o sistema é levado pra um nível de energia maior.
Além da distância, o número de elétrons na eletrosfera dos íons também importa.
Por isso a gente calcula aquele valor de de acordo com o “gás nobre que o íon imita”. Quanto mais elétrons, maior o que a gente calcula, que tá ligado com a repulsão das eletrosferas.
Passo 3
Agora a curva azul.
A curva azul representa, de fato, a energia do sistema de acordo com a distância entre os ions.
Ela é uma soma simples das outras duas curvas.
A gente pode perceber que em valores muito pequenos de a repulsão é “mais importante” que a atração, e o sistema tem uma energia total alta.
Conforme aumenta, a repulsão vai diminuindo e a atração passa a ser o fator mais importante.
O ponto onde a energia do sistema é mínimo é o ponto de estabilidade máxima. Essa é a distância que os íons “gostam de ficar” (a natureza prefere ficar em estados de baixa energia, lembra?). Essa distância é o e a energia do sistema no é, justamente, a energia do retículo cristalino, ou seja, .
A partir de aumentar o até diminui a repulsão, mas também diminui a atração e “enfraquece a ligação”, ou seja, aumentar a distância aumenta a energia do sistema (em azul).
Passo 4
Resumindo: quando as cargas estão infinitamente separadas, a energia entre elas é zero.
Conforme a gente vai aproximando as duas, tanto a atração quanto a repulsão aumenta.
Repulsão leva o sistema para um estado mais energético.
Atração leva para um estado menos energético (“ligado”).
A energia do sistema é a soma desses dois fatores: atração e repulsão.
No ponto de energia mínima, temos a energia do retículo cristalino, que é a energia do sistema quando as cargas estão distantes por , o comprimento da ligação no retículo cristalino.
Resposta
Ei, a resposta está no passo a passo :)