A figura abaixo mostra parte do ciclo de Born-Haber para a formação do a partir de seus constituintes. Sabendo que a seta menor indica um consumo de de energia e, a seta maior, a liberação de de energia, responda:
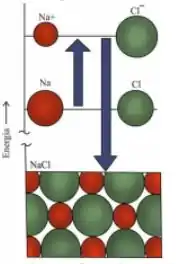
a) A que processo corresponde os valores de energia indicados pelas setas no ciclo? Escreva a equação química correspondente a essas duas transformações, indicando os estados físicos de reagentes e produtos.
b) Calcule a entalpia padrão de formação para o , utilizando os dados termoquímicos que forem necessários.
c) Os sólidos iônicos e formam o mesmo tipo de estrutura cristalina, logo eles tem o mesmo valor para a constante de Madelung. Em qual composto as interações entre os íons são mais fortes? Justifique.
Passo 1
a) A primeira seta está partindo do e indo para o . Esse processo corresponde a ionização do sódio. E a energia correspondente a é a 1ª energia de ionização do sódio, que é definida pela perda de um elétron no estado gasoso. Então a equação química com os estados físicos fica assim:
A seta maior está partindo do sódio catiônico + cloreto e indo pro sal. Essa etapa corresponde a formação do sólido cristalino, à qual corresponde a enegia de rede ou do retículo cristalino (). Nessa etapa, tanto o cátion quanto o ânion estão no estado gasoso e formam um sólido.
Passo 2
b) Pelo enunciado a gente sabe que a seta menor, ou seja, a ionização do sódio, consome 496 kJ/mol e a energia do retículo cristalino corresponde a liberação de 787 kJ/mol.
Pra calcular a entalpia padrão de formação (), precisamos de outros dados (que devem ser fornecidos).
- Energia de sublimação do sódio metálico: kJ/mol
- Energia de dissociação da molécula de cloro: kJ/mol
- Entalpia de ganho de elétron do cloro: kJ/mol
Caso seja dada a afinidade eletrônica ao invés da entalpia de ganho de elétrons, não esquece que uma é o oposto da outra, valeu? Você precisa do valor da entalpia!
E como a gente usa meio mol de pra fazer um mol de átomos de , aquela energia de dissociação vai entrar na nossa conta pela metade!
kJ/mol
Como o caminho pra formar o sólido iônico não interessa no cálculo da energia, pela Lei de Hess e segundo o ciclo de Born Haber:
Passo 3
c) A interação entre os íons é de natureza eletrostática.
A força eletrostática é proporcional ao módulo das cargas e inversamente proporcional ao quadrado da distância entre elas.
Isso é o mesmo que dizer que quanto maior a carga dos íons, maior é a interação entre eles. Quanto maior a distância entre os íons, menor a interação entre eles.
A gente também pode percerber isso pelo cálculo da energia do retículo cristalino:
Quanto maior o módulo de , mais forte é a interação entre cátions e ânions no sólido iônico.
E é diretamente proporcional à carga dos íons e inversamente proporcional à distância entre eles.
Como o enunciado nos diz que a constante de Madelung (A) é a mesma para e , podemos nos concentrar no raio e nas cargas desses caras para prever qual sólido terá interações mais fortes.
A carga do é igual a carga do . Então o fator determinante tem que ser o raio!
Como o está um período abaixo do na tabela periódica, o tem um nível da eletrosfera preenchido a mais que o .
Por isso, o raio atômico do é maior que o do , e o raio iônico do é maior que o raio iônico do .
Como, quanto maior o raio, menor a interação entre os íons, pode-se dizer que as interações no são mais fortes do que as interações no .
Resposta
a) Seta menor:
Seta maior:
b)
c) Como, quanto maior o raio, menor a interação entre os íons, pode-se dizer que as interações no são mais fortes do que as interações no .