Considere a função de transferência de um sistema a tempo contínuo:
Para os valores do parâmetro , esboce no plano complexo o lugar das raízes da equação característica , em função do ganho .
Passo 1
O exercício pede para esboçar o lugar das raízes de , usando dois valores distintos de : e . Para fazermos o que o exercício pede, usaremos duas funções do MATLAB. Primeiro, vamos usar a função para entrar com . Em seguida, usaremos para plotar o lugar das raízes de .
Faremos esse procedimento duas vezes: uma vez para e outra vez para .
Passo 2
O primeiro passo é definir no MATLAB, usando a função , que tem a sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Contudo, repare que o denominador de está fatorizado. Para definirmos , vamos dividi-la em duas partes, e , de forma que :
Vamos começar definindo em um script novo do MATLAB, cujo numerador é e o denominador é . Vamos criar duas variáveis contendo os coeficientes dos polinômios de . A primeira variável representará os coeficientes do polinômio do numerador e será chamada de . A segunda variável será um vetor chamado e terá os coeficientes do polinômio do denominador. Após criar as duas variáveis de entrada de , digite o comando :

Desta forma, a função de transferência é criada e armazenada na variável
Vamos fazer a mesma coisa para , começando com , definido por meio do comando :

Os vetores e contêm os coeficientes dos polinômios do numerador e do denominador de , respectivamente. Com a função , cria-se a funções de transferência .
Finalmente, para definir , inclua em seu código o produto abaixo:
![]()
Execute o programa para ver a cara de , com :

Passo 3
Após definir para , use a função para plotar o lugar das raízes. tem a sintaxe:
A função tem como entrada uma função de transferência criada a partir do comando (no nosso caso, é a variável ). Ao executarmos o programa, gera um gráfico com o lugar das raízes da função de transferência.
Adicione no seu script o comando:
![]()
Ao executar o programa, você terá o gráfico do lugar das raízes de , quando :
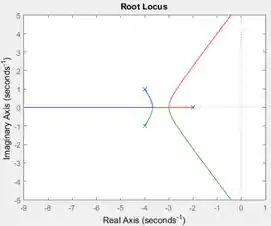
Passo 4
Vamos fazer o mesmo procedimento para . No seu código, troque o valor da variável de para , lá onde você criour :

Desta forma, ficará com essa cara:

E o lugar das raízes ficará assim:
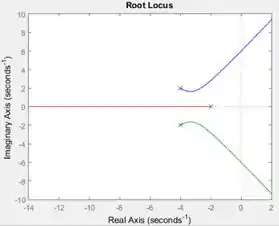
Resposta
:
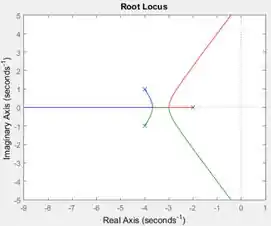
: