Um processo pode ser definido pela seguinte função de transferência:
Onde e são as constantes de tempo da válvula de controle e do transmissor, respectivamente. Encontre a faixa de ganho da malha para a qual a malha é estável se e .
Passo 1
O enunciado nos dá uma função de transferência e nos pede para determinar a faixa de valores que o ganho de um controlador proporcional pode assumir, de forma que a malha seja estável.
Para determinarmos os valores de , plotaremos o lugar das raízes de no MATLAB, usando a função , e acharemos os valores de no próprio gráfico.
Antes disso, entraremos com no MATLAB, por meio da função .
Passo 2
Antes de tudo, vamos informar ao MATLAB as constantes de tempo das válvulas: e . Abra um script novo e digite:
![]()
A variável armazena e a variável , .
Agora, vamos entrar com a função de transferência , usando , que tem a sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Contudo, repare que o denominador de está fatorizado. Logo, para podermos pegar os coeficientes dele, precisamos expandi-lo (isto é, multiplicar os termos) para gerarmos o polinômio. Por isso, antes de usarmos , faremos uma manipulação algébrica com o denominador de .
Passo 3
Faremos a manipulação algébrica do denominador no MATLAB mesmo. No script onde você definiu e , digite as linhas de código:

Na primeira linha, criamos uma variável simbólica .
Na segunda linha, entramos com o denominador de , armazenando-o na variável .
Na terceira linha, usamos o comando do MATLAB em . Este comando multiplicará os termos de e gerará o polinômio que precisamos, armazenando-o em .
Rodando o programa, temos:
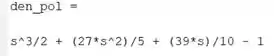
Passo 4
Agora que temos o polinômio do denominador de , podemos criar os vetores que servirão de entrada para . Para , o polinômio do numerador é . Já o polinômio do denominador é .
No mesmo script onde você obteve , crie duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:
![]()
Em seguida, adicione o comando abaixo para criar :
![]()
A função de transferência é armazenada na variável . Você pode ver como ficou ao rodar o programa e pedir ao MATLAB para imprimir no Command Window:

Note que as frações do denominador foram convertidas em números decimais, por isso que o denominador está um pouquinho diferente de . Apesar da forma diferente, é exatamente a mesma coisa.
Passo 5
Após criar , usaremos a função para plotar o lugar das raízes. tem a sintaxe:
A função tem como entrada uma função de transferência criada a partir do comando (no nosso caso, é a variável ). Ao executarmos o programa, gera um gráfico com o lugar das raízes da função de trasnferência.
Adicione no seu script o comando:
![]()
Ao executar o programa, você terá o gráfico do lugar das raízes de :

Passo 6
Podemos encontrar a faixa de valores que pode assumir no gráfico gerado no passo . Para isto, devemos relembrar o critério de estabilidade: uma malha de controle é estável se as raízes forem números reais negativos ou se forem números complexos com a parte real negativa. No lugar das raízes, isso significa que as raízes devem estar à esquerda do eixo vertical.
Isso quer dizer que, para encontrarmos os valores do ganho que garantem a estabilidade, devemos analisar os ramos que cruzam o eixo vertical. Logo, no nosso gráfico, a área de interesse é essa aqui:

Por isso, recomendo você ampliar o gráfico, dando um zoom nessa região, pra ver bem certinho os polos e os ramos. Você pode dar o zoom clicando no botão destacado em vermelho abaixo:

Para ver os valores de ganho, selecione o botão “Data Cursor” (destacado em azul acima) e clique sobre um dos ramos. Aparecerá um quadradinho preto com uma janelinha contendo informações sobre na naquele ponto:
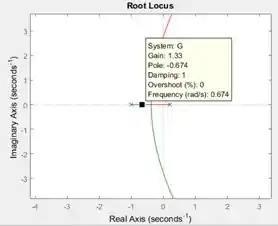
O dado “Gain” é o que nos interessa. Ele representa o ganho nesse ponto. Se você arrastar o quadradinho até um xizinho, que representa um polo, você verá que quando o cursor estiver sobre o polo. Logo, quanto mais perto do polo, menor o .
Repare que existe um polo à direita do eixo vertical, equivalente a :

Como em esse polo é um número real positivo, que leva à instabilidade, a faixa de valores que o ganho deve assumir para que a malha seja estável não pode começar em . Para definirmos qual o valor mínimo de , devemos ver quanto ele vale exatamente sobre o eixo vertical, ou o mais próximo possível do eixo vertical que o MATLAB nos permita. Arraste o quadradinho preto sobre o ramo vermelho, sobre sua parte horizontal, e você terá:
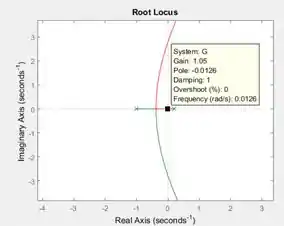
No ponto marcado acima, o polo se torna um número real negativo com um ganho .
Para identificar o valor máximo que pode assumir, continue arrastando o quadradinho preto sobre o ramo vermelho até que o ramo cruze novamente o eixo vertical, no limite em que a parte real do polo continue negativa:
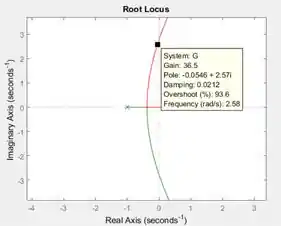
Temos que o valor máximo que pode assumir é .