Esboce o lugar geométrico das raízes para o sistema mostrado abaixo:
Passo 1
O exercício pede para traçar o lugar das raízes de . Para fazermos o que o exercício pede, usaremos duas funções do MATLAB. Primeiro, vamos usar a função para entrar com . Em seguida, usaremos para plotar o lugar das raízes de .
Passo 2
O primeiro passo para resolver o exercício é entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Abra um script novo no MATLAB e crie dois vetores, um contendo os coeficientes de e outro contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:
![]()
O vetor contém os coeficientes do numerador e o vetor , do denominador de .
Em seguida, adicione o comando abaixo para criar :
![]()
A função de transferência é armazenada na variável . Você pode ver como ficou ao rodar o programa e pedir ao MATLAB para imprimir no Command Window:

Passo 3
Após criar , usaremos a função para plotar o lugar das raízes. tem a sintaxe:
A função tem como entrada uma função de transferência criada a partir do comando (no nosso caso, é a variável ). Ao executarmos o programa, gera um gráfico com o lugar das raízes da função de trasnferência.
Adicione no seu script o comando:
![]()
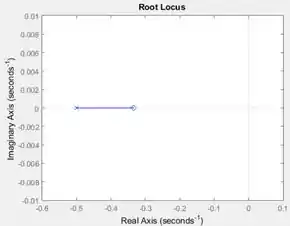
Ao executar o programa, você terá o gráfico do lugar das raízes de .
Resposta