Seja
Plote o lugar das raízes e ache os polos e os zeros de .
Passo 1
O exercício pede para plotar o lugar das raízes de e, a partir do gráfico do lugar das raízes, identificar os polos e os zeros da função de transferência. Lembrando que os zeros são as raízes do numerador de , isto é, de . Como se trata de um polinômio de grau, temos que identificar dois zeros no lugar das raízes.
Já os polos são as raízes do denominador de , isto é, de . Como se trata de um polinômio do grau, existem quatro polos no lugar das raízes.
Para plotarmos o lugar das raízes, usaremos duas funções do MATLAB. Primeiro, vamos usar a função para entrar com no MATLAB. Em seguida, usaremos para plotar o lugar das raízes de .
Passo 2
O primeiro passo para resolver o exercício é entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script do MATLAB, crie dois vetores, um chamado de que contém os coeficientes de e outro chamado , contendo os coeficientes de . Ambos os vetores vão do coeficiente do elemento com maior expoente ao coeficiente de menor expoente:
![]()
Em seguida, adicione o comando abaixo para criar :
![]()
A função de transferência é armazenada na variável , isto é, é igual a . Você pode confirmar isso rodando o programa e pedindo ao MATLAB para imprimir no Command Window:

Passo 3
Após criar , usaremos a função para plotar o lugar das raízes. tem a sintaxe:
A função tem como entrada uma função de transferência criada a partir do comando (no nosso caso, é a variável ). Ao executarmos o programa, gera um gráfico com o lugar das raízes da função de trasnferência.
Adicione no seu script o comando:
![]()
Ao executar o programa, você terá o gráfico do lugar das raízes de :
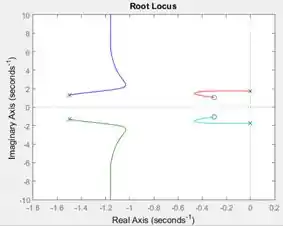
Passo 4
Podemos identificar os zeros e os polos no gráfico do lugar das raízes. Os zeros são representados por bolinhas e os polos, por xizinhos. Para sabermos quanto os zeros e os polos valem, podemos clicar sobre os ramos do gráfico. Aparecerá um quadradinho preto com um quadro com dados sobre o ponto onde você clicou. Esse quadradinho pode ser arrastado ao longo dos ramos até atingir um polo ou um zero.
Vamos começar com os zeros, que vou chamar de e . Repare que o gráfico tem duas bolinhas: isso porque o numerador é um polinômio de grau, logo, ele possui duas raízes. Vamos clicar nos ramos vermelho e azul piscina para aparecer o quadradinho preto e vamos arrastá-lo até as bolinhas:
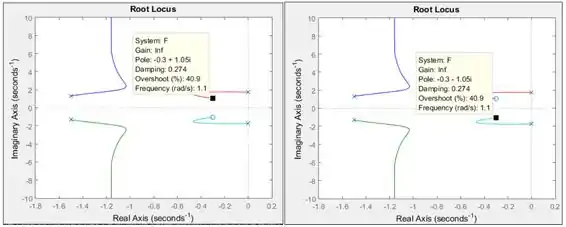
Você terá certeza que chegou no zero quando o dado for igual a . Temos que os zeros de são:
Vamos agora identificar os polos. Temos quatro xizinhos no gráfico, representando os quatro polos de , que vou chamar de , , e . Existem quatro polos pois o denominador de é um polinômio de grau, isto é, ele possui quatro raízes. Clique nos quatro ramos para aparecer o quadradinho preto e arraste-o até cada um dos xizinhos:
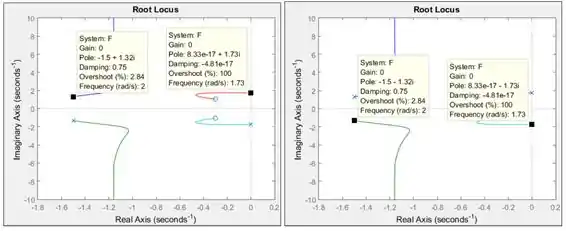
Você terá certeza que chegou no polo quando o dado for igual a . Temos que os polos de são:
Os polos e estão sobre o eixo vertical, logo, eles são números puramente complexos, com parte real igual a . Pelo que está indicado na figura acima, eles têm um resíduo na parte real de . É um número tão pequenininho, que podemos considerar igual a . Logo, os outros dois polos de são:
Resposta

Os zeros de são: e
Os polos de são: