Considere o sistema de controle com realimentação unitária apresentado abaixo, no qual se assume . Para a função de transferência definida a seguir:

- Esboce o lugar das raízes em função do ganho .
- Determine de maneira que os polos dominantes do sistema em malha fechada apresentem fator de amortecimento igual a .
- Para determinado no item anterior, encontre a saída para uma entrada degrau unitário.
Passo 1
O enunciado nos dá uma função de transferência e nos pede para esboçar o lugar das raízes, determinar o ganho de modo que os polos dominantes tenham fator de amortecimento igual a (lembrando que os polos dominantes são aqueles que estão mais próximos do eixo imaginário do lugar das raízes, ou seja, do eixo vertical) e, usando o encontrado, determinar a saída do sistema para o degrau unitário.
Para plotar o lugar das raízes de no MATLAB e resolver a letra a do exercício, usaremos a função . A partir do lugar das raízes obtido na letra a, resolveremos a letra b, achando o valor de no próprio gráfico. Com a resposta da letra b, faremos a letra c, gerando o sistema em malha fechada por meio do comando e plotando a resposta ao degrau unitário por meio da função .
Passo 2
O primeiro passo é entrar com por meio da função , que tem a sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Contudo, repare que o numerador e o denominador de estão fatorizados. Para definirmos no MATLAB, vamos quebrá-la em três partes, , e , de forma que :
Vamos começar definindo em um script novo do MATLAB, cujo numerador é . Já o denominador é o polinômio . Vamos criar duas variáveis contendo os coeficientes dos polinômios de . A primeira variável representará os coeficientes do polinômio do numerador e será chamada de . A segunda variável será um vetor chamado e terá os coeficientes do polinômio do denominador. Após criar as duas variáveis de entrada de , digite o comando :

Desta forma, a função de transferência é criada e armazenada na variável
Vamos fazer a mesma coisa para e :

Os vetores e contêm os coeficientes do polinômio do numerador de e , respectivamente. Já os vetores e contêm os coeficientes do polinômio do denominador de e , respectivamente. Com a função , criam-se as funções de transferência e .
Finalmente, para definir , inclua em seu código o produto abaixo:
![]()
Execute o programa para ver como ficou:

Passo 3
Após definir , podemos resolver a letra a do exercício usando a função para plotar o lugar das raízes. tem a sintaxe:
A função tem como entrada uma função de transferência criada a partir do comando (no nosso caso, é a variável ). Ao executarmos o programa, gera um gráfico com o lugar das raízes da função de transferência.
Adicione no seu script o comando:
![]()
Ao executar o programa, você terá o gráfico do lugar das raízes de :
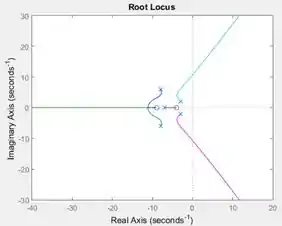
Pronto! Esta é a resposta da letra a =D
Passo 4
A partir do gráfico do lugar das raízes, vamos resolver a letra b do exercício, que pede para encontrarmos o ganho de maneira que os polos dominantes do sistema em malha fechada apresentem fator de amortecimento igual a .
No gráfico do lugar das raízes do MATLAB, as bolinhas representam os zeros e os chizinhos, os polos. Para vermos os parâmetros de nos polos dominantes, devemos clicar sobre os ramos partindo dos chizinhos mais próximos do eixo vertical, como no print abaixo:

Veja que abriu uma janelinha apresentando algumas propriedades da função de transferência no ponto onde clicamos. É nessa janelinha que vamos ver o valor de , dado pelo parâmetro “Gain”, e o fator de amortecimento, que é dado pelo parâmetro “Damping”. No caso do print acima, para um ganho , temos um fator de amortecimento de .
Arraste o quadradinho preto que apareceu onde você clicou até encontrar um ponto onde o parâmetro “Damping” seja igual a :

Temos que um ganho nos dá um fator de amortecimento igual a nos polos dominantes. Letra b resolvida ;D
Passo 5
A letra c pede para encontrarmos a resposta de para um degrau unitário, considerando o ganho encontrado na letra b. Para isto, usaremos o comando , que tem a sintaxe:
A função plota o gráfico da resposta ao degrau unitário de , que é uma função de transferência criada usando o comando .
Contudo, precisamos aplicar no sistema em malha fechada, como o diagrama do enunciado:
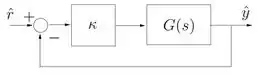
Para criar um sistema em malha fechada no MATLAB, usamos o comando , que tem a sintaxe:
O comando tem como entrada duas funções de transferência e retorna a função de transferência equivalente ao diagrama de blocos abaixo:

A primeira entrada de é a função de transferência da parte de cima do diagrama e a segunda entrada, é a função de transferência da parte de baixo.
No caso do exercício, quando usarmos a função , teremos que a primeira entrada é e a segunda entrada é , pois se trata de um sistema com realimentação unitária.
Insira no seu código as duas linhas abaixo:
![]()
Na primeira linha, entramos com o ganho encontrado na letra b.
Na segunda linha, usamos o comando para plotar a resposta ao degrau do sistema com realimentação unitário, modelado por meio do comando .
Execute o programa e você terá a resposta da letra c.

