O caixote de está parado quando a força é aplicada. Determine a aceleração resultante do caixote se , e .
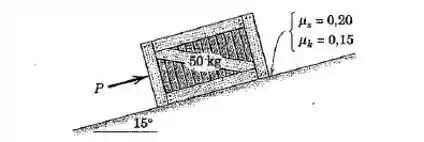
Passo 1
O sistema da figura vamos pode ser descrito por:
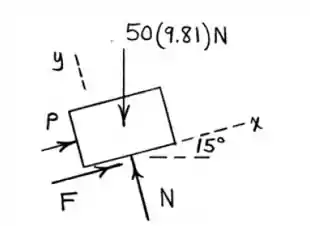
Temos a força , a força de atrito , a força normal e o peso .
Passo 2
a)
Para , vamos ter o seguinte equilíbrio no eixo perpendicular ao plano:
E a resultante na direção vale quanto? Vamos, primeiro, calcular o módulo da força de atrito estática máxima:
E quanto vale a componente do peso? Vale
Como podemos ver, a força peso na direção do plano inclinado tem valor maior do que . Assim, ocorrerá deslizamento e o atrito atuante será cinético:
Passo 3
b)
O equilíbrio vertical continuará o mesmo, já que atua na direção do plano:
Agora vamos analisar a força resultante na direção do plano:
Lembra da força de atrito máxima? Vale:
Como:
A força não consegue vencer a força de atrito: Não há deslocamento:
Passo 4
c)
Vamos fazer a mesma coisa:
E:
Como:
Vai haver movimento, dado por:
Resposta
a)
b)
c)