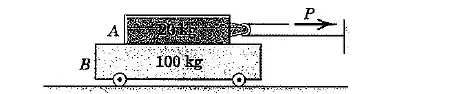
Se os coeficientes de atrito estático e dinâmico entre o bloco de e o carrinho de têm ambos essencialemente o mesmo valor de , determine a aceleração de cada parte para e .
Passo 1
a)
Vamos primeiro analisar o bloco Temos duas forças atuando nesse corpo:
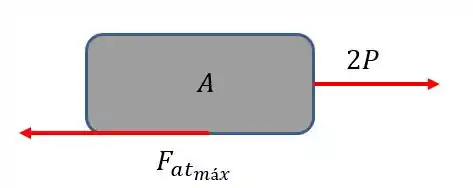
Por que vale Porque existe uma roldana, o que duplica a força.
E quanto vale
Basta usarmos:
Onde é o módulo da força normal que exerce em . Essa força, no caso, é o peso de
Assim:
E assim:
Perceba que:
Passo 2
Vamos assumir que ocorre deslizamento: que tem uma aceleração diferente de e que, por isso, se desloca sobre . Nesse caso, não podemos considerar os dois corpos como um só. Assim:
Vamos calcular a aceleração de
Agora vamos calcular a aceleração de
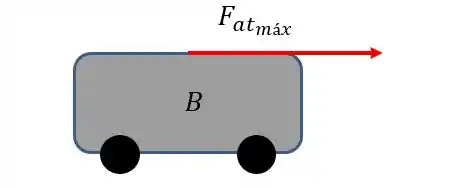
só sofre a ação da força , já que não possui atrito com o solo( já que possui rodinhas). Assim:
Agora veja:
Ou seja, o bloco se desloca em cima de
Passo 3
b)
Nesse caso, o continua sendo o mesmo. No entanto:
Sendo assim, como a força não é suficiente para vencer a força de atrito, não ocorre o deslizamento. Isso quer dizer que podemos tratar o conjunto dos dois corpos como um só:
Assim:
Resposta
a)
b)