Movimento Espacial
Teoria
Introdução
Você já aprendeu bastante coisa sobre movimentos, porém estávamos sempre restritos a uma ou duas dimensões. Mas e se tivermos um caso de uma montanha russa, por exemplo, o que devemos fazer?
Vamos ter que expandir para três dimensões e para isso vamos precisar de eixos coordenados apropriados.
Neste capítulo vamos conhecer sistemas de coordenadas para descrever movimentos em três dimensões. Vamos lá!
Coordenadas retangulares
As coordenadas retangulares são bem intuitivas para gente, são os eixos
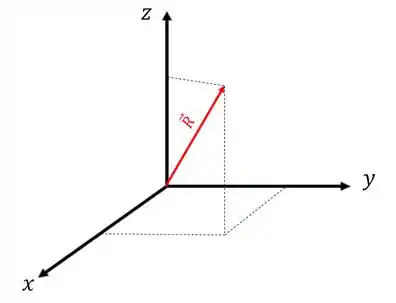
A posição de um ponto nesse sistema vai ter uma componente em cada um dos eixos e o vetor é dado por:
E a velocidade? A derivada disso em relação ao tempo:
E a aceleração? Só derivar de novo:
Basicamente isso!
Repare que para três dimensões vamos usar a notação no lugar de .
Coordenadas Cilíndricas
O sistema de coordenadas cilíndricas possui três vetores unitários: o vetor na direção do eixo , o vetor na direção do raio e perpendicular a este o vetor que aponta no sentido de crescimento do ângulo.
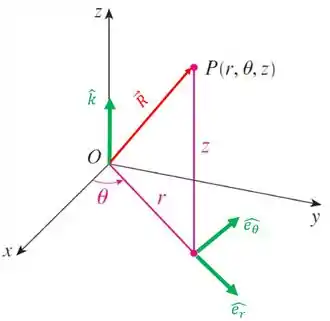
Para localizar qualquer coisa nas coordenadas cilíndricas precisamos de três informações: a altura , o raio do cilindro e o ângulo que ele faz com um eixo de referência. Assim, para o vetor posição vamos ter:
Para achar o vetor velocidade temos que derivar a expressão de . Mas antes temos que lembrar que a derivada no tempo de é:
Então, a velocidade será:
Se separarmos as componentes vamos ter:
Então, para calcular o módulo da velocidade será:
Para compreendermos melhor: é a taxa com a qual o raio cresce, é a taxa de variação angular e a taxa de crescimento de
Seguindo esse mesmo raciocínio, vamos obter a fórmula para aceleração que é:
Vamos separar as componentes:
Com isso, o módulo da aceleração será:
Coordenadas Esféricas
Vamos utilizar coordenadas esféricas quando tivermos que usar um raio e dois ângulos () para indicar a posição de um corpo.
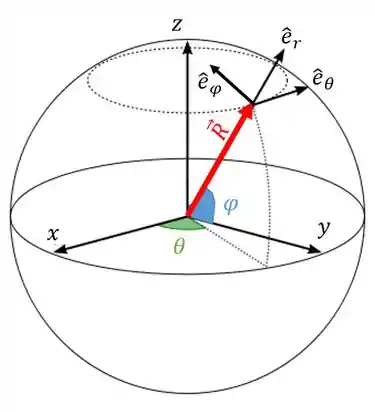
Nesse caso, a velocidade pode ser descrita pelo vetor:
E a aceleração é dada por:
Onde:
E:
Esse último sistema é bem complicado, né? Não se preocupe, os dois primeiros que são mais importantes e são eles que vamos praticar nos exercícios.
Bora lá!
Coordenadas Cilíndricas
Coordenadas Esféricas
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 62, 2/172
Um projétil é lançado a partir do ponto com uma velocidade inicial de módulo , direcionado como indicado na figura. Calcule as componentes , e da posição, velocidade e aceleração segundos após o lançamento. Despreze o arrasto aerodinâmico.
Passo 1
Perceba o seguinte: a velocidade de lançamento faz um ângulo de com o plano (horizontal). Já no plano , a velocidade faz um ângulo de com o eixo , no sentido negativo de
Vamos desenhar separadamente:
E:
Beleza?
O que podemos concluir já de cara?
Bom, não é dito no enunciado, mas esse sistema está sendo influenciado pela gravidade local. Essa gravidade atua no eixo .
Sendo assim, o movimento do corpo será acelerado na direção , mas será um movimento de velocidade constante tanto em quanto em
Passo 2
Vamos primeiro calcular as equações gerais da posição, velocidade e aceleração para cada direção e depois calculamos para
Para
Onde
E:
Assim:
Substituindo os valores:
Dê uma olhada aqui no triângulo:
Beleza. E a posição vai ser dado por:
Já que a aceleração é constante e igual a
, já que ele parte da origem. Assim:
Passo 3
Agora vamos lidar com as posições e
Já que os movimentos terão velocidades constantes. Vamos olhar de novo a direção da nossa velocidade nesse plano:
Beleza, mas eu posso pegar a velocidade que ele deu no enunciado ( e fazer:
e ?
Não!!!
Antes disso, precisamos calcular a componente horizontal de . A componente vertical é , que já calculamos. Assim, a horizontal será:
Agora sim:
E as equações do movimento?
Serão assim:
Onde:
E:
Então, vamos ter que:
E:
Passo 4
Assim:
Para
E:
Como:
E:
E também:
Então:
Formalizando isso vetorialmente:
E:
E para finalizar:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 63, 2/176
O elemento giratório em uma câmara de mistura recebe um movimento axial periódico enquanto está girando na velocidade angular constante . Determine a expressão para o módulo máximo da aceleração de um ponto sobre a borda de raio . A frequência da oscilação vertical é constante.
Passo 1
Vamos usar as coordenadas polares ( neste exercício.
Perceba que existe aceleração em Sim, a aceleração de um movimento harmônico.
E em Não! Perceba que o movimento circular ao redor do eixo de giro é feito sob uma velocidade constante.
Existe aceleração no sentido radial? Sim, como é um movimento circular, vai existir uma aceleração centrípeta.
Passo 2
Desenhando:
Passo 3
Vamos equacionar agora:
Perceba que o raio não varia, assim: Então:
E:
Como já discutimos.
E:
Show? Só derivamos duas vezes o movimento harmônico que tá rolando na vertical.
Passo 4
Assim, o módulo da aceleração é dado por:
E qual será o módulo máximo? Ocorrerá quando . Assim:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 63, 2/178
Uma aeronave decola em e se eleva em um ângulo constante com inclinação de para no plano vertical com uma velocidade constante . A aeronave é rastreada por radar em . Para a posição , determine os valores de , e .
Passo 1
Bom, vamos primeiro desenhar esse sistema mostrando as variáveis pertinentes:
é o ângulo que o avião faz com a horizontal. Ele vale:
E
Usamos os dois triângulos da figura.
Passo 2
Para acharmos , primeiro decompomos usando (assim obtemos a velocidade vertical):
Após isso, decompomos na direção de
Ou seja:
Assim:
Pra achar , temos duas formas: primeiro usando a fórmula e segundo percebendo que a velocidade horizontal em é a própria
Percebeu? É só ver que ela tem uma tendência a girar ao redor do eixo central. Sendo assim:
Onde é o raio de giração.
Opa! Sacou o motivo de eu ter dividido o por Para transformar pra . Queremos achar , que é dada em . Assim:
Passo 3
Agora pra achar vamos seguir o mesmo procedimento: A velocidade seguindo a direção do ângulo pode ser dada por:
Ou, se você perceber, essa velocidade nada mais é que a componente vertical da velocidade em
Mas quem vai ser o Ou seja, o raio de giração?
Vai ser a hipotenusa do triângulo maior da figura. Como é o cateto adjacente, teremos:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 64, 2/180
O pequeno bloco movimenta-se com velocidadeconstante na trajetória circular de raio sobre a superfície inclinada. Se no instante , determine as componentes , e da velocidade e da aceleração como funções do tempo.
Passo 1
Opa, essa é uma questão que assusta a primeira vista, né?
Veja bem: ele tá te pedindo as componentes e da aceleração e velocidade daquele móvel. Porém, e você deve ter percebido, o móvel está executando uma trajetória em um plano inclinado.
E agora?
É só usarmos os novos eixos e :
Depois a gente vai usar relações trigonométricas pra transferir o que calcularmos para as coordenadas retangulares padrão.
Além disso, veja que, pelo o enunciado, a velocidade tangencial vale . Assim, a velocidade angular vai ser:
E
Guarde no coração, vamos usá-las no final.
Passo 2
Beleza, nesse novo sistema de coordenadas, vamos ter:
Assim:
E é nulo nesse novo sistema de coordenadas. Esse sistema está em cima do plano inclinado. Assim, a componente é nula.
Assim:
Perceba que usamos a regra da cadeia ali.
E:
Passo 3
Vamos como vamos decompor essas componentes na direção agora. Dê uma olhada na figura abaixo:
A linha azul tracejada indica o plano inclinado.
Bom, assim, teremos que decompor tanto o eixo quanto o . Assim:
Substituindo:
Substituindo
E Vai ser parecido, mas vamos ter uma subtração, já que as projeções terão sentidos opostos:
Faltou o . O que fazemos com ele? Nada, . O plano inclinado não influencia a direção pois ela é perpendicular a ele:
Passo 4
Tudo pronto, agora só falta a gente derivar pra achar
E:
E:
E:
E o
E:
E:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 63, 2/179
O esguicho rotativo borrifa uma grande área circular e gira com a velocidade angular constante . Partículas de água deslocam-se ao longo do tubo em uma taxa constante em relação ao tubo. Escreva expressões para os módulos da velocidade e aceleração de uma partícula de água para uma determinada posição no tubo rotativo.
Passo 1
Bom, o que está acontecendo ali é que essa mangueira está esguichando água enquanto gira.
Sua missão é encontrar as expressões para a velocidade da partícula e para a sua aceleração.
Bora?
Basicamente vamos identificar as variáveis importantes e aplicar as fórmulas.
Passo 2
é a taxa de variação do deslocamento da partícula na direção de Temos, então, que a velocidade radial de uma partícula será dada por:
Sendo
E
E a velocidade em Será:
Percebeu que decompomos ali o pra achar
Assim, o módulo da velocidade será:
Passo 3
Para as acelerações, teremos:
A variação de , que nada mais é que a variação de , é constante, assim:
E:
E:
Só que , já que , que é uma constante. Assim:
E só falta
Assim, o módulo da aceleração será dado por:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 63, 2/183
A estrutura de base da escada de um carro de bombeiros gira em torno de um eixo vertical através de com uma velocidade angular constante . Ao mesmo tempo, a unidade da escada se eleva a uma taxa constante , e a seção da escada se prolonga de dentro da seção na taxa constante de . No instante em questão, , e Determine o módulo da velocidade e da aceleração da extremidade da escada.
Passo 1
Vamos usar as coordenadas esféricas aqui.
Primeiro, vamos calcular
E:
E só falta:
Assim:
Passo 2
Em relação às acelerações:
E:
Assim:
Assim: