Movimento Retilíneo
Produzido por Pablo RicardoTeoria
O Movimento retilíneo, como o próprio nome indica, é aquele que acontece em trajetória reta, como o movimento de um carro em linha reta. Ele pode ser tanto um movimento vertical, como horizontal que é o que vamos focar aqui!
Pra começarmos com tudo, se liga nesse vídeozinho super completo que o Responde Aí preparou pra você sobre Movimento Retilíneo na Dinâmica 👇
📢 Clique para saber mais:
Posição e Deslocamento
Imagine um carro andando em uma estrada... Para localizarmos esse carro vamos usar o que chamamos de posição
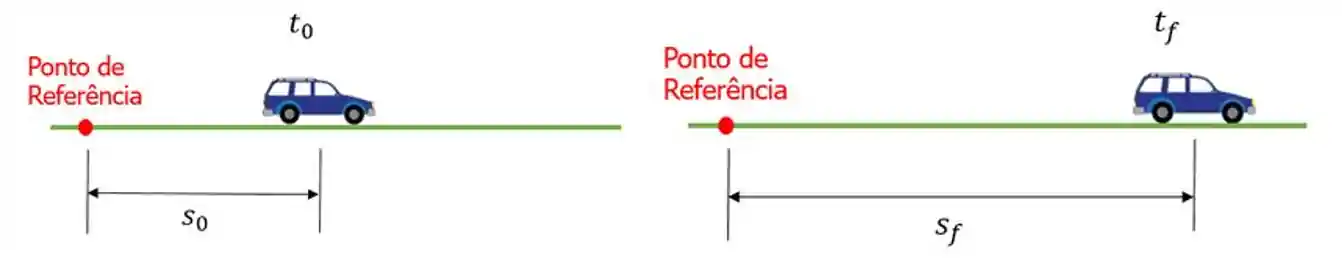
Repare que no primeiro instante de tempo
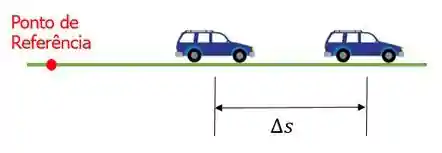
Sempre que analisarmos a posição de qualquer coisa, após escolhermos um ponto de referência, temos que escolher um sentido para ser positivo e outro para ser negativo. Dessa maneira, o deslocamento será positivo se o objeto andar no sentido positivo e será negativo se ele andar no sentido negativo que escolhemos.
Velocidade
Se eu falar para você que ontem eu dirigi a uma velocidade de
Chamamos de velocidade média a razão entre o deslocamento e intervalo de tempo no qual esse deslocamento ocorreu, ou seja, o quanto eu percorri com meu carro em um determinado intervalo de tempo:
Mas e se eu quiser saber a minha velocidade exatamente em uma posição? Para isso, vamos usar o conceito de velocidade instantânea que é quando
A velocidade instantânea é obtida a partir da derivada da posição em relação ao tempo. Se observarmos o gráfico de deslocamento versus tempo, percebemos que a derivada é igual a inclinação da reta tangente à curva em um instante
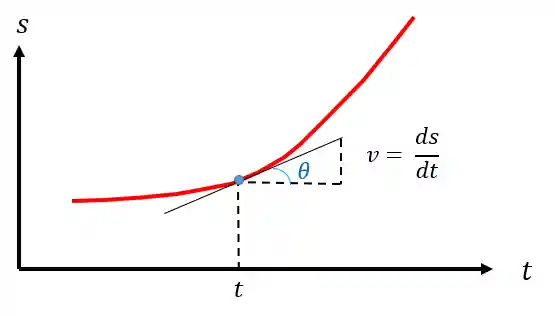
Aceleração
Vamos chamar de aceleração média o quanto a velocidade de um corpo variou dentro de um intervalo de tempo:
Podemos calcular a aceleração instantânea também, para isso derivamos a velocidade em relação ao tempo:
A aceleração é positiva se a velocidade estiver aumentando e será negativa se a velocidade estiver diminuindo. Quando a velocidade está diminuindo falamos que o corpo está desacelerando.
Gráficos
Aqui no movimento retilíneo, é muito importante saber interpretar e tirar as informações importantes dos gráficos aqui no Movimento Retilíneo! Então bora começar com o gráfico de velocidade?!
No gráfico da velocidade em função do tempo, temos que a área embaixo da curva é igual ao deslocamento
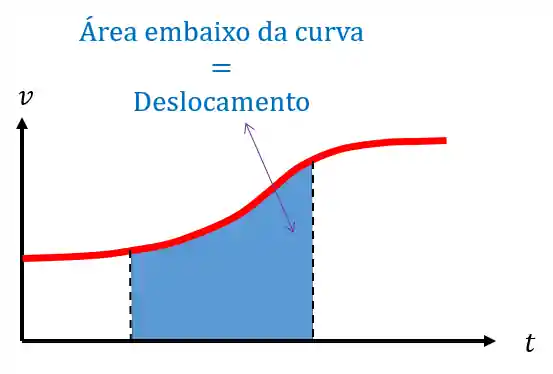
Pra a gente conseguir calcular essa área vamos precisar usar as integrais! Primeiro pegamos a fórmula da velocidade e isolamos o
E integramos dos dois lados:
Agora é só resolver a integral e como resultado você terá o deslocamento!
Outro gráfico importante é o de aceleração, dessa vez a sua área embaixo da curva vai nos dar a velocidade média.
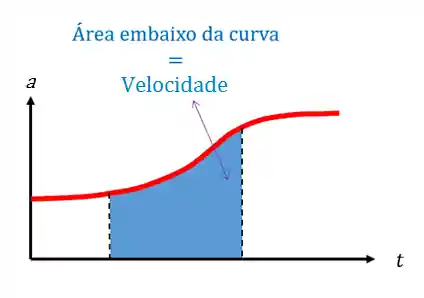
Achamos a velocidade integrando a fórmula de velocidade instantânea, assim como fizemos ali em cima:
Pra achar a velocidade é só integrar e correr pro abraço!
Fórmulas do Movimento Retilíneo
Pra encerrar com chave de ouro, bora ver um resuminho das fórmulas do Movimento Retilíneo?!
Movimento Retilíneo Uniforme (MRU)
- Velocidade média:
- Velocidade Instantânea:
Movimento Retilíneo Uniformemente Variado (MRUV)
- Aceleração Média:
- Aceleração Instantânea:
- Função horária da velocidade:
- Função horária da posição:
- Equação de Torricelli:
Bora praticar com exercícios?!