Coordenadas Polares, Tangenciais e Normais
Produzido por Pablo RicardoTeoria
Introdução
Imagina que eu quero calcular o módulo da velocidade do carinha aqui embaixo em relação ao chão:
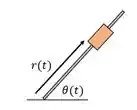
Onde temos que e , no instante em que . Pensando no que a gente viu na teoria passada, a gente poderia tentar escrever o vetor posição, decompondo como no desenho abaixo
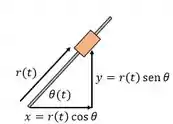
Então como vai ficar o nosso vetor posição?
E agora como faz para obter a velocidade? Só derivar esse amigo aí! Pô vai dar um trabalhão isso aí. Será que não tem um jeito mais fácil de fazermos essa conta?
Claro que tem! É para isso que serve o que chamamos de coordenadas polares. Vamos conhecer melhor isso aí!
Coordenadas Polares
Nessas coordenadas a gente cria dois vetores unitários perpendiculares entre si:
- Um na direção do raio da trajetória e que vamos chamar de ;
- Outro que é tangente à trajetória e que vamos chamar de .
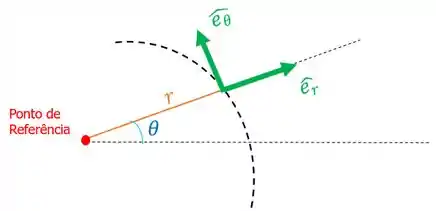
E quando eu sei que tenho que usar coordenadas polares? Dê preferência por usar estas coordenadas quando você tiver:
- Uma trajetória curvilínea;
- Um ponto de referência fixo em volta do qual o corpo gira;
- E quando a questão te der um ângulo que o corpo faz com relação à horizontal.
Então, sempre vamos colocar a equação da posição e a equação do ângulo em função das coordenadas polares, assim:
Nós aprendemos que a velocidade é a derivada do deslocamento com relação ao tempo. Mas como fazemos para derivar os vetores unitários e com relação ao tempo? Vamos ter o seguinte:
Lembrando que o pontinho em cima do ângulo indica derivada primeira.
Então, a velocidade é:
Vamos separar os componentes para visualizarmos melhor:
Para calcularmos o módulo da velocidade:
Vamos ver agora a aceleração. Nós vimos que a aceleração é a derivada da velocidade no tempo. Então, vamos seguir o mesmo raciocínio:
Não esqueça que os dois pontinhos em cima da variável indicam que é derivada segunda.
Para facilitar, vamos separar a aceleração nas suas componentes:
Então, o módulo da aceleração será:
Vamos resolver o exemplo inicial usando coordenadas polares para entendermos melhor.
Primeiro, vamos posicionar nossas coordenadas:
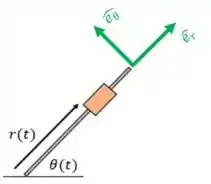
Agora vamos escrever a equação da posição e a equação do ângulo em função das coordenadas polares, assim:
O que a questão pede é o módulo da velocidade quando . Vamos calcular a velocidade então:
Vamos calcular primeiro e que é só derivar as expressões de e de em função do tempo:
Substituindo na expressão da velocidade:
Como ele quer no tempo , vamos ter:
Vamos calcular o módulo agora:
Show! Ficou bem mais fácil! Então, quando você tiver problemas em que for fácil escrever a distância entre o seu objeto e algo fixo e o ângulo dessa distância, a boa é usar coordenadas polares.
Agora vamos ver outro tipo de coordenada muito utilizada.
Coordenadas Tangenciais e Normais
Nessas coordenadas, os nossos vetores unitários perpendiculares entre si vão ser:
- Um normal à trajetória cujo sentido positivo vai ser sempre apontando para o centro da curva e que vamos chamar de;
- Outro tangente à trajetória cujo sentido positivo aponta para o sentido de crescimento do deslocamento e que vamos chamar de .
- Quando não tiver um ponto de referência fixo;
- Quando não tiver um ângulo com relação à horizontal;
- Quando conhecemos toda a trajetória, por exemplo se for um círculo.
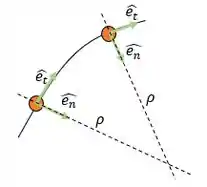
Vamos chamar o raio da curvatura de .
Repare que esse sistema de coordenadas não é fixo, ele tem sua origem no corpo que está se movendo e vai andando junto com o corpo.
E quando vou usar as coordenadas tangenciais e normais? Dê preferência por usar estas coordenadas:
Agora vamos utilizar essa nova coordenada para descrever a velocidade. Sabemos que a velocidade é sempre tangente à trajetória, então a velocidade vai ser sempre na nossa direção tangencial:
Onde, o módulo da velocidade é:
E a aceleração? Sabemos que é só derivar a velocidade em função do tempo. Mas como fica a derivada do vetor unitário ? Fica assim:
Então, a aceleração vai ser:
Podemos escrever:
Com isso, dizemos que a aceleração tem uma componente tangencial e outra normal.
A gente aprendeu no ensino médio que a aceleração que muda a velocidade, certo? Então um objeto que se move com velocidade constante tem aceleração zero, né? Errado!
Olha ali na expressão da aceleração: se o módulo da velocidade é constante, a gente vai ter que:
Ou seja, não tem componente tangencial da aceleração. Mas, se o corpo estiver fazendo uma curva, essa trajetória tem um raio ! Então eu vou ter componente normal da aceleração! Ou seja, cada componente da aceleração vai ter uma função:
- Componente tangencial muda o módulo da velocidade e é sempre tangente à trajetória. Vamos chamar esta componente de aceleração tangencial e seu módulo é:
- Componente normal muda direção e o sentido da velocidade e sempre aponta para o centro da trajetória. Vamos chamar esta componente de aceleração centrípeta e seu módulo é:
O módulo do vetor aceleração é:
Um corpo com velocidade constante não tem aceleração tangencial, mas todo corpo que esteja fazendo um movimento curvo vai sempre ter aceleração centrípeta.
O sistema de coordenadas tangenciais e normais é muito usado para descobrir o raio de curvatura, , da trajetória. Em outros casos, os exercícios pedem para calcular a aceleração do corpo. Mas isso não é regra, é só uma dica.
Beleza! Agora vamos praticar para pegar o jeito da coisa!
Coordenadas Tangenciais e Normais
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 45, 2/101
Um carro de teste parte do repouso em uma pista horizontal circular de de raio e aumenta sua velocidade a uma taxa uniforma para atingir os em segundos. Determine o módulo da aceleração total do carro segundos após a partida.
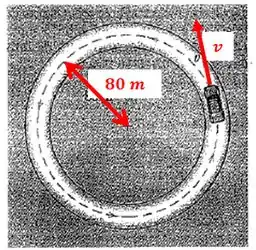
Passo 1
Vamos primeiro calcular a aceleração média do carro. Podemos fazer isso da seguinte forma:
Perceba que a velocidade está em Vamos dividir por para passar para :
Assim:
Assim, a velocidade tangencial em função do tempo pode ser dada por:
Passo 2
Beleza, então a velocidade para o tempo
Assim, podemos calcular a aceleração centrípeta:
Passo 3
Assim, a aceleração total é dada por:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 43, 2/115
Na parte inferior da acrobacia aérea na qual o avião descreve um círculo em um plano vertical, o módulo da aceleração total do avião é de . Se a velocidade do avião em relação ao ar é de e está aumentando na taxa de por segundo, calcule o raio de curvatura da trajetória em .
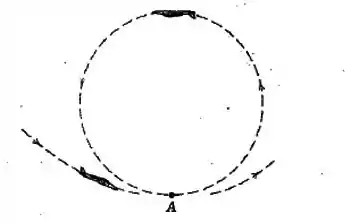
Passo 1
Nessa questão, vamos lidar com acelerações:
- Aceleração total:
- Aceleração tangencial :
- Aceleração normal:
Perceba que ele está pedindo o raio de curvatura, sendo assim, teremos que lidar com a aceleração normal.
Passo 2
A aceleração tangencial pode ser calculada através de:
A variação de velocidade é dada por:
Isso está acontecendo em um intervalo de tempo
Passo 3
Agora, perceba que o enunciado disse que o módulo da aceleração total vale
Passo 4
Assim, podemos dizer que a aceleração normal será:
Passo 5
Então:
Sendo que:
Assim:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 55, 2/147
O foguete é lançado verticalmente e rastreado pela estação de radar mostrada. Quando chega a , outras medições correspondentes fornecem os valores , , . Calcule o módulo da velocidade e da aceleração do foguete nesta posição.
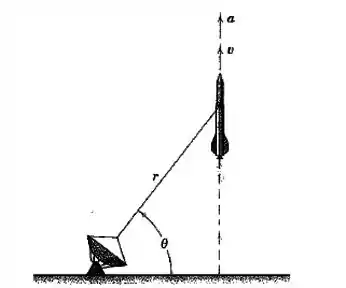
Passo 1
As velocidades nas coordenadas polares são:
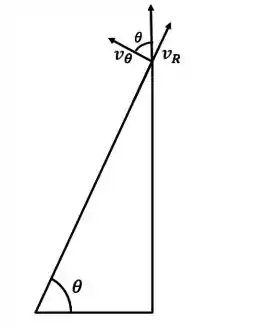
Como sabemos:
Além disso, olhando para o triângulo acima do triângulo maior:
Passo 2
E as acelerações total e radial são:
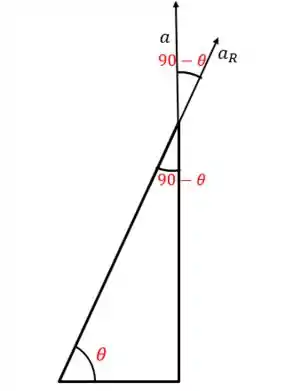
Usando:
Passo 3
Agora, veja que:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 55, 2/153
Na parte inferior de uma acrobacia aérea na qual o avião descreve um círculo em um plano vertical () a uma altitude de metros, o avião tem uma velocidade horizontal de e nenhuma aceleração horizontal. O raio de curvatura da trajetória é . Para o radar de rastreamento em , determine os valores de e registrado para esse instante.
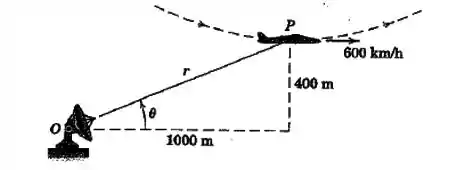
Passo 1
Vamos primeiro desenhar esse sistema mostrando os ângulos de interesse:
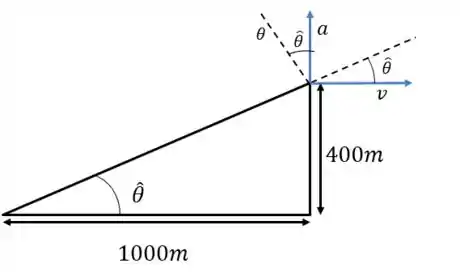
Quem é a aceleração É a aceleração centrípeta do avião, já que ele está descrevendo uma curva. E é a velocidade do próprio avião.
Quanto vale
E
Passo 2
Bom, a velocidade nós temos que passar para :
Com isso, podemos calcular a aceleração centrípeta:
Vamos calcular primeiro :
Já que é a taxa de crescimento ou decrescimento do raio Vamos ter que decompor na direção
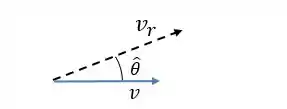
Assim:
E é a velocidade na direção
Só que:
Passo 3
E a aceleração radial? Da mesma forma que a velocidade radial, podemos usar seno e cosseno para calcular:
Só que:
Então:
Passo 4
E a aceleração na direção Será:
Lembrando que:
Assim:
Resposta
Exercício Resolvido #5
J.L. Meriam& L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 55, 2/137
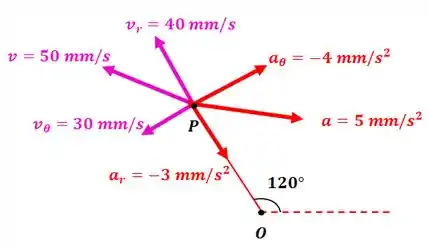
O movimento do bloco deslizando na ranhura radial rotativa é controlado pelo parafuso como mostrado. Para o instante representado , e . Além disso, o parafuso gira a uma velocidade constante fornecendo . Para este instante, determine os módulos da velocidade e da aceleração de . Desenhe e a para .
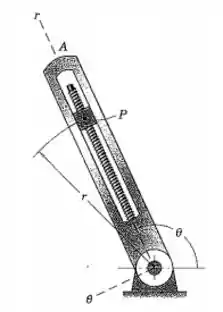
Passo 1
Temos:
E:
Então:
Passo 2
E:
E:
Assim:
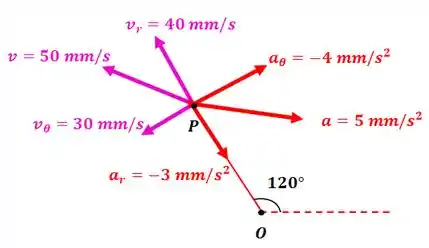
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 55, 2/137
Um motorista que dirige ao longo de um trecho de reta de uma rodovia diminui a velocidade de seu automóvel para uma taxa constante antes de sair da rodovia em direção a uma rampa de saída circular com raio de . Ele continua a desaceleração com a mesma taxa constante de tal forma que, após ter entrado na rampa, sua velocidade escalar diminuiu para , uma velocidade escalar que ele, então, mantém. Sabendo que a essa velocidade constante a aceleração total do carro é igual a um quarto de seu valor antes de entrar na rampa, determine o valor máximo da aceleração total do carro.
Passo 1
Como temos um trecho circular, vamos usar a abordagem com coordenadas tangenciais e normais. Para isso, vamos usar a expressão:
Passo 2
Durante toda a frenagem a aceleração tangencial é constante, porque ele diz que o piloto diminui a velocidade com uma taxa constante. Então o valor máximo para a aceleração acontece no ponto onde a componente normal é máxima.
Como a trajetória é circular, o raio de curvatura é constante e igual a . Então, a componente normal será máxima quando for máximo.
Agora onde isso ocorre? Lembra que estamos freando o carro? Então a velocidade máxima ocorre no ponto inicial, ou seja, imediatamente depois que ele entra na curva!
Resumindo, precisamos descobrir o valor de e da velocidade no ponto de entrada da curva!
Passo 3
Depois que ele fica com velocidade constante a gente tem:
Como a trajetória é circular . Além disso, ele contou que nesse ponto
Logo,
Passo 4
Como o enunciado nos disse:
Passo 5
Antes dele frear o carro, ele estava num trecho reto. Isso é o mesmo que dizer que , ou seja:
O sinal de menos é porque estamos freando! Então, temos que
Passo 6
Para , temos que , então:
Assim,
E no início da curva, :
Passo 7
Então, a aceleração máxima ocorre imediatamente depois que ele entra na curva e vale: