Binário, Torçor e Resultante
Teoria
Introdução
Você já viu como calcular um sistema equivalente força-binário em duas dimensões. Além disso, você viu como achar a posição da resultante das forças através desse sistema.
Agora imagine que você tem uma placa retangular fininha, onde estão atuando todas essas forças aqui:
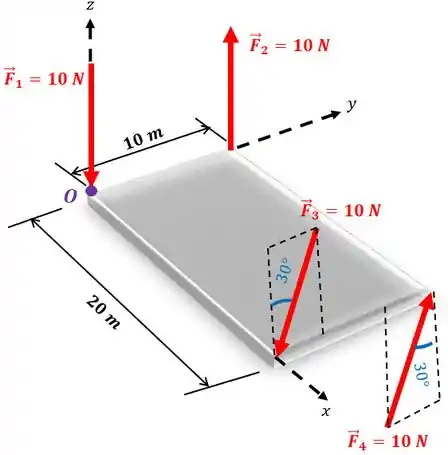
Como você faria para representar esse sistema de forças por um binário e uma força resultante no ponto ?
Parece mais complicado, não é? Confesso que é um pouquinho, meu amigo, mas estaremos juntos nessa!
Sistema força-binário equivalente em 3D
Quando a nossa intenção é representar um sistema de forças por uma resultante em um ponto, a primeira coisa que você tem que fazer é definir cada uma dessas forças. No nosso exemplo, temos as seguintes forças:
E:
A segunda coisa que você precisa fazer é calcular a resultante das forças:
Pra fazer isso, basta somar as componentes termo a termo:
Repare que todas as nossas forças tem o mesmo módulo e se anulam!
E o momento? Bom, como vimos, o binário equivalente representa a soma de todos os momentos em relação ao ponto de referência.
Então, o momento equivalente do nosso exemplo com relação ao ponto será:
Agora que são elas: qual a melhor maneira de calcular cada momentinho desses? Como vimos no capítulo anterior, é através do produto vetorial:
Sendo assim, você vai precisar definir cada um dos vetores . Mas isso é bem simples, pois esses são braços de alavanca, ou seja, a distância do ponto de aplicação da força em relação ao ponto de referência.
Então, no nosso exemplo, temos que calcular o momento que cada força faz cm relação ao ponto :
- Força : repare que a linha de ação da força passa pelo ponto , então o vetor é zero:
- Força : o vetor vai ser:
- Força : o vetor é:
- Força : o vetor é:
Então, o momento da força também é zero:
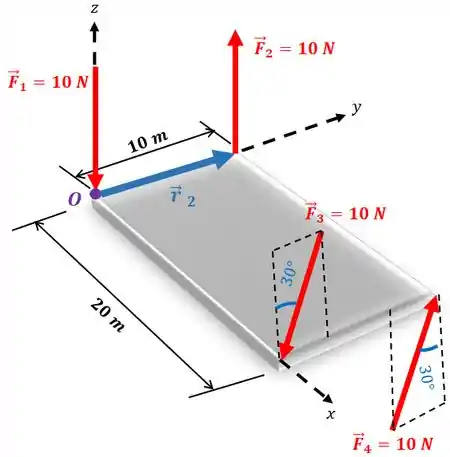
E o momento de com relação ao ponto será:
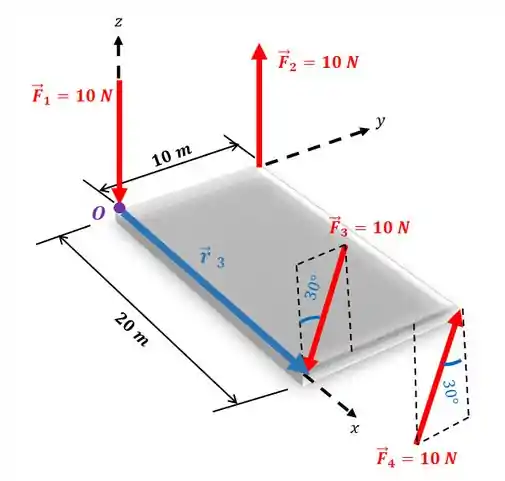
Então, o produto vetorial fica:
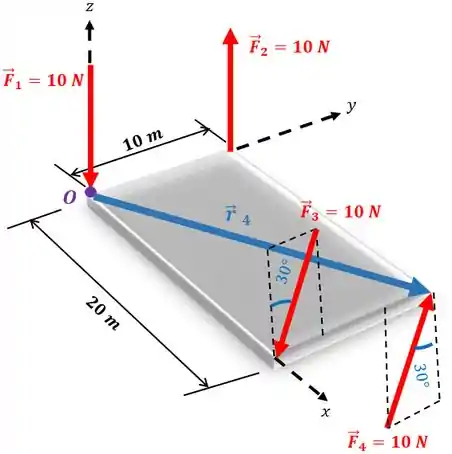
O produto vetorial fica assim:
Então, o momento resultante no ponto será a soma de cada um desses momentos que calculamos:
Observação: é claro que podemos calcular os momentos através do momento que cada componente exerce em relação a cada eixo, como vimos no capítulo anterior. Mas de uma forma geral, fazendo vetorialmente a gente tem mais chances de acertar.
Torçor e Resultante
Além do sistema equivalente força-binário, você também pode representar um sistema de forças por um torçor e uma força resultante.
Um torçor é quando o momento resultante é paralelo à força resultante. Um torçor é positivo se os vetores momento e força resultante apontam no mesmo sentido e negativo se eles apontam em sentidos opostos.
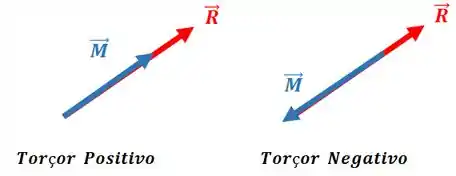
Como assim? Bem, imagine que temos uma resultante e um binário representados no ponto abaixo:
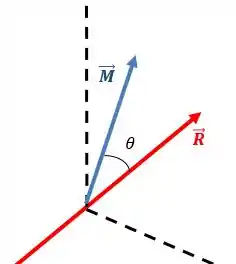
O momento faz um certo ângulo com a força, sendo que ambos pertencem ao mesmo plano vertical. Então, podemos decompor esse momento em uma componente paralela a e uma perpendicular:
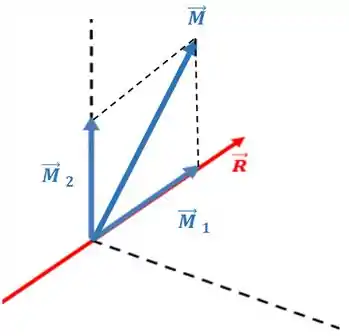
Show de bola? E se você somar a esse sistema duas forças: e , separadas por uma distância ?
A primeira conclusão é que a resultante das forças continua a mesma (), afinal de contas é como se você tivesse somado e a alguma conta.
Então vamos ver:
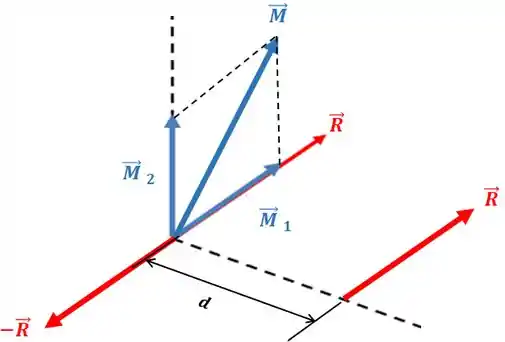
Repare que as duas forças iniciais se anulam e sobra só aquela força afastada em unidades. Além disso, lembra que o binário é um vetor livre, que pode ser representado em qualquer ponto? Vamos deslocar a componente para cima da força que sobrou:
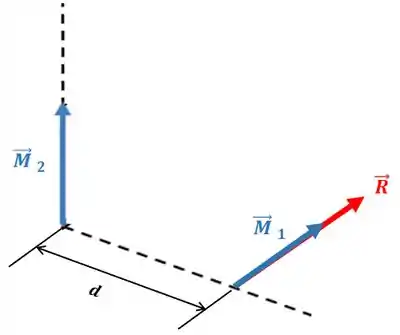
Uma dúvida que você pode ter é: quanto vale para que possamos excluir o e representar tudo com o torçor? Bom, perceba que exerce um momento em relação a esse ponto inicial agora, pois está afastado por uma distância .
Como o que fizemos foi uma manipulação, é de se esperar que não exista um momento “extra” por causa desse deslocamento. Sendo assim, o módulo do momento que faz em relação ao ponto inicial tem que ser
Ou, vetorialmente:
E o torçor? Como vimos, é esse amiguinho aqui:
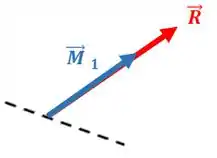
Tá, mas e como a gente equaciona isso tudo? Bom, lembra do in��cio que:
Substituindo a nova relação que achamos para
Show? Basicamente, é o momento resultante do sistema e é o momento associado ao torçor (que tem a mesma direção que ). Você pode encontrar essa equação escrita assim também:
Resolvendo uma questão sobre torçor
E se o enunciado te pedir pra achar o torçor associado àquele sistema?
Bom, você vai seguir um caminho mais ou menos assim:
- Se o momento e a força resultante do sistema ainda não estiverem calculados, você vai calculá-los, seguindo tudo que usamos antes. Isso é o mesmo que calcular o sistema força-binário equivalente.
- De posse do vetor da força resultante, você vai escrevê-lo no formato abaixo:
- Você não sabe o módulo do torçor, , nem quem é o vetor . Mas você sabe qual é a direção de : A mesma de , representada pelo vetor
- Resolva o produto e depois some ao vetor Você vai chegar numa equação com as variáveis e .
- Agora é só igualar a equação com o vetor momento resultante do início:
Ou seja, o módulo do vetor força vezes um vetor direção . Como se faz isso? Bom, primeiro você calcula o módulo de
Sendo
De posse desse valor, você vai multiplicar e dividir o vetor força por ele:
Repare que isso não afeta nossa força. Mas você pode estar se perguntando: isso não vai alterar nada? Mas não é que vai! Olha só isso aqui, é a mesma coisa que tínhamos antes:
Só que, como é a própria força dividida pelo módulo, podemos dizer que esse é o vetor normalizado:
Aí chegamos ao que queríamos:
Show? Basicamente, calcule o módulo da força e divida cada componente dela pelo seu módulo. Esse vetor vai ser importante na hora de definir o torçor, já que ele tem a mesma direção da força resultante!
E você pode escrever o vetor de forma genérica, assim:
Você vai chegar a um sistema com variáveis. Aí é só resolver!!!
Observação muito importante:
Algumas vezes, o vetor do momento resultante será perpendicular ao vetor força resultante:
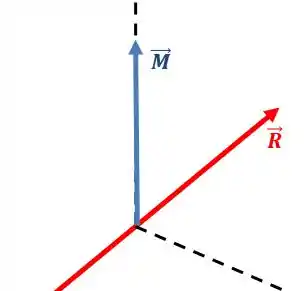
Nesse caso, não existirá uma componente do momento que seja paralela à força. O que isso significa?
Significa que não existirá um momento associado ao torçor. Ou seja, você até pode representar a força resultante a uma certa distância do ponto de referência, mas será apenas uma força, sem um momento associado:
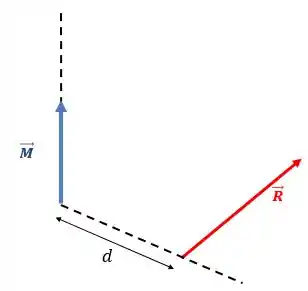
Pra resolver esses problemas, você vai usar a equação:
Como você tem o valor da força resultante e do momento resultante, você consegue achar
E é basicamente isso, mas não se preocupe, vamos fazer alguns exercícios. Bora praticar?
Torçor e Resultante
Resolvendo uma questão sobre torçor
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 76,2/169
As direções de rotação dos eixos de entrada e de saída no redutor de engrenagens estão indicadas pelas setas curvadas tracejadas. Um torque de entrada (binário) de é aplicada ao eixo na direção da rotação. O eixo de saída fornece um torque de à máquina que ele controla (que não está mostrada). O eixo da máquina exerce um torque de reação igual e contrário no eixo de saída do redutor. Determine a resultante dos dois binários que atuam no redutor e calcule o cosseno diretor de em relação ao eixo
Passo 1
Temos dois binários na figura: um deles está na direção e outro na direção
Porém, não sabemos o sentido dos vetores.
Vamos usar, então, a regra da mão direita pra saber o sentido de cada um.
Passo 2
Usando a regra:
Perceba que o momento no eixo aponta no sentido negativo do eixo e que o momento no eixo aponta no sentido negativo desse seu eixo. Sendo assim:
Passo 3
Agora queremos achar o cosseno diretor de em relação ao eixo . Vamos antes desenhar o vetor no plano , visto de cima:
Beleza! Agora vamos calcular o módulo do vetor
Assim, o cosseno diretor é dado pelo cosseno do triângulo retângulo que o vetor faz com os eixos. Assim, podemos calcular ele assim:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 73,2/159
Determine o sistema força-binário em que seja equivalente às duas forças aplicadas ao eixo . é perpendicular a Nesse caso, determine as coordenadas no plano por onde passa resultante do sistema de forças.
Passo 1
Vamos primeiro calcular a resultante das forças. Veja que elas possuem uma característica em comum: ambas fazem um ângulo com o eixo
Podemos definir a força de assim:
Podemos definir a força de assim:
Assim, a força resultante é dada por:
Passo 2
Agora vamos calcular o momento que cada uma faz em relação ao ponto
Perceba que as distâncias são dadas apenas no eixo . Então, vamos fazer o produto vetorial para cada força.
Para a força , o vetor distância é:
Assim, o produto vetorial fica:
Para a força , o vetor distância é:
Então, o produto vetorial fica:
Assim, o momento total em relação ao ponto
Pronto, com a força resultante e esse momento, definimos o sistema força-binário equivalente em
Passo 3
Sendo:
Vamos ver se os vetores são perpendiculares. Para isso, vamos efetuar o produto escalar:
Como o produto é diferente de zero, eles não são perpendiculares.
Assim, podemos representar a resultante por um conjunto torçor.
Vamos escrever a força resultante na forma:
Assim:
Passo 4
Queremos agora achar o ponto onde a resultante pode ser representada, junto com o seu torçor:
Vamos usar, então, a relação:
é o momento do torçor e, portanto, tem a mesma direção que a força resultante:
Passo 5
Vamos desenvolver: