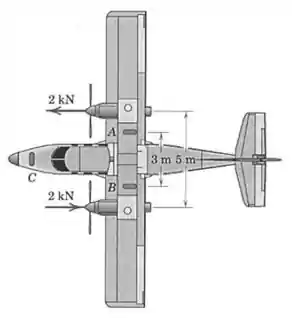
Como parte de um teste, os dois motores de um avião são acelerados e as inclinações das hélices são ajustadas de modo a resultar em um empuxo para frente e para trás, como mostrado. Que força deve ser exercida pelo chão em cada uma das duas rodas principais freadas em e , para se opor ao efeito giratório dos empuxos das duas hélices? Despreze quaisquer efeitos da roda no nariz, , que está girada de e não está freada.

Dê uma olhada no par de forças de . Elas têm a mesma direção e sentidos opostos, o nome disso é binário (quando duas forças não geram uma força resultante mas sim apenas um momento resultante), podemos calcular o momento associado a ele usando a seguinte fórmula:

Onde é a distância entre os pontos de aplicação das duas forças e é o módulo de cada uma:

Nesse caso ainda podemos dizer que esse binário gera um momento no sentido horário.