A força de é aplicada sobre a manopla da válvula de controle hidráulico, como mostrado. Calcule o momento dessa força em relação ao ponto
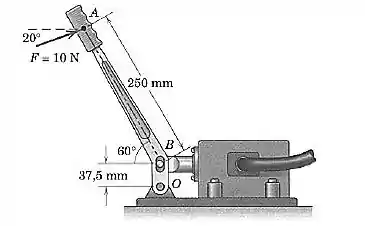
Passo 1
Diferentemente daquele outro exercício em que a barra também possuía um ângulo e nós resolvemos isso por meio de um ângulo relativo, nesse vamos fazer de uma forma mais bruta mesmo, só pra aprendermos duas formas diferentes.
O sistema do problema pode ser simplificado na figura abaixo:
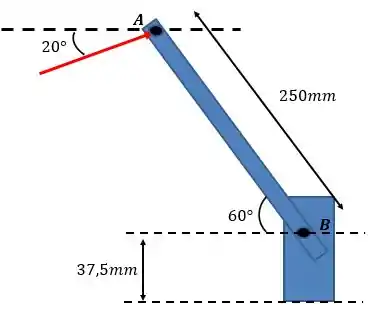
Passo 2
Vamos aplicar o teorema de Varignon, mas dessa vez vamos decompor a força e as distâncias.
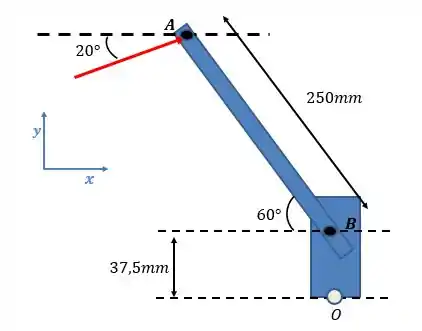
Decompondo a força na componente e as distância na componente :
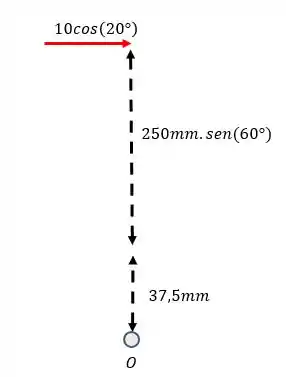
Adotando o sentido horário como o positivo, esse momento é igual a:
Passo 3
Decompondo a força na direção vertical e a distância na direção horizontal:
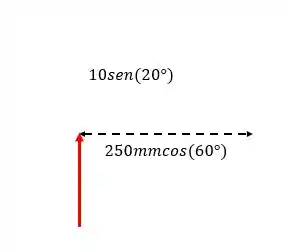
Assim:
Assim, o momento resultante vai ser a soma dos dois( já que eles têm o mesmo sentido):