Um mecânico puxa a chave de boca de com a força de mostrada. Determine o momento da força em relação ao centro do parafuso.
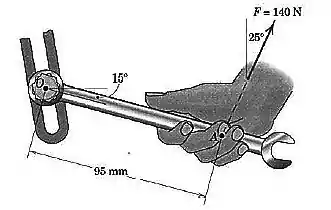
Passo 1
Vamos ter que pensar um pouco mais nessa questão aqui:
O problema dessa questão é que a barra de tem uma inclinação em relação à horizontal. É interessante, então, se a gente pudesse modelar esse problema sem essa inclinação.
Como assim?
Trabalhando com uma inclinação relativa.
Vamos chamar essa inclinação de
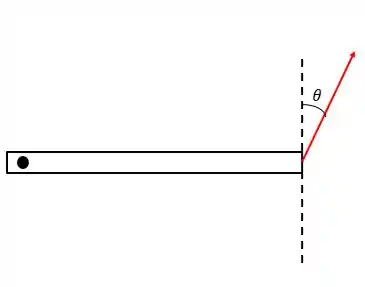
Passo 2
No desenho acima, não existe uma inclinação horizontal. Agora vamos inclinar a barra e ver o que acontece com a inclinação do vetor força lá na ponta da barra:
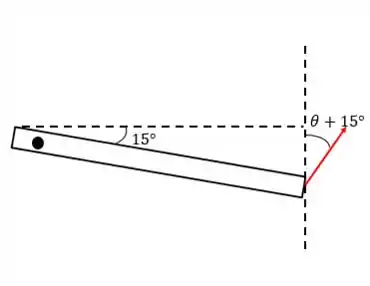
Com o giro de , a força também se inclina em a mais. Pelo enunciado, sabemos que esse ângulo final vale , assim:
Passo 3
Assim, podemos trabalhar com esse sistema:
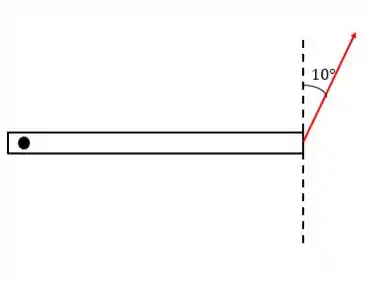
A componente () produzirá um momento nulo. Então vamos usar apenas a componente vertical. Assim: