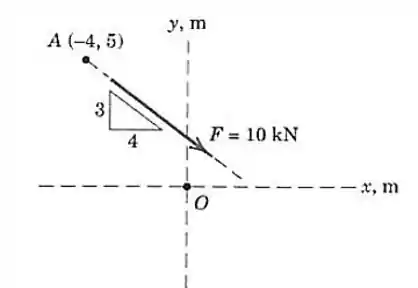
A força de é aplicada no ponto . Calcule o momento de em relação ao ponto . Determine os pontos nos eixos e em relação aos quais o momento de vale zero.
Passo 1
Vamos começar decompondo a força nos eixo e . Para isso temos que achar o ângulo de inclinação dessa força:
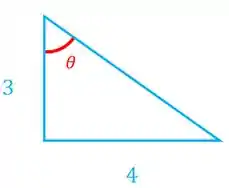
Agora podemos decompor a nossa força :
Passo 2
Agora vamos calcular o momento com relação ao ponto para cada uma das componentes separadamente. Vamos começar pela componente em :
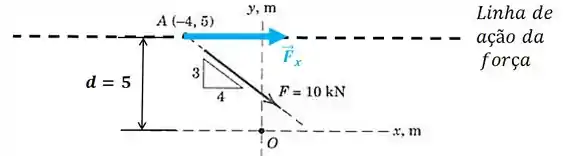
A distância perpendicular à linha de ação da força até o ponto é:
Então, o módulo do momento de com relação ao ponto é dado pelo módulo da força e a distância:
E para saber o sinal, temos que analisar...
Repare que a força gira no sentido horário em torno do ponto , então ela será negativa pela nossa convenção de sinais:
E a componente em ?
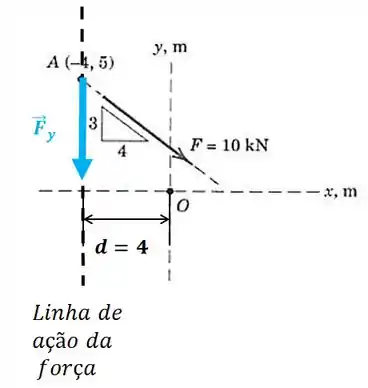
O módulo do momento desta força será:
E esse momento será positivo ou negativo? Repare que a força tende a girar em torno do ponto no sentido anti-horário, logo ela será positiva.
O momento total em relação ao ponto será igual a soma do momento que cada componente faz:
Ou seja, como esse valor deu negativo, o nosso momento total está no sentido horário!
Passo 3
Agora temos que ver onde nos eixos e o momento será zero. Pessoal, momento não é calculado como força vezes distância?
Então é só acharmos os pontos onda a distância da linha de ação da força ao eixo é zero!
Isso ocorre onde a linha de ação da força cruza esses eixos:
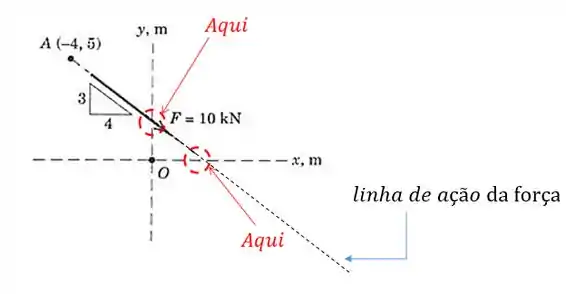
Repare que agora vamos utilizar a linha de ação da força e não mais apenas de suas componentes e .
Então, vamos usar semelhança de triângulos para obter esses valores. Vamos começar pelo eixo :
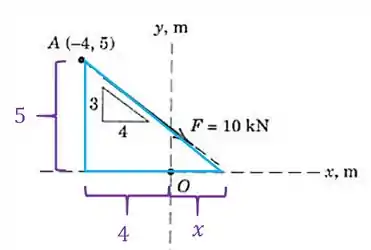
Vamos fazer a semelhança entre esses dois triângulos aqui:
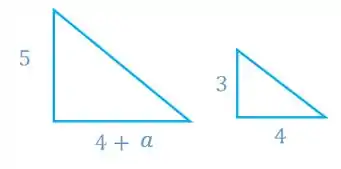
Então, a coordenada fica:
Ou seja
Vamos fazer outra semelhança de triângulos para achar o ponto onde intercepta o eixo :
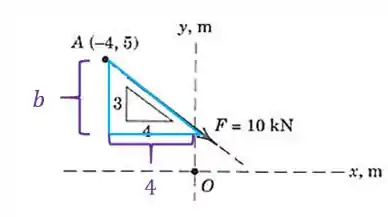
Vamos ter os seguintes triângulos:
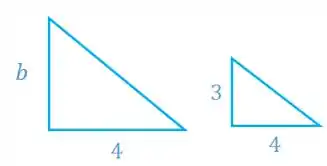
Então, a coordenada fica:
Repare que para achar esse valor também poderíamos ter feito a semelhança de triângulos usando 2,67. Ficaria assim:
Ou seja,