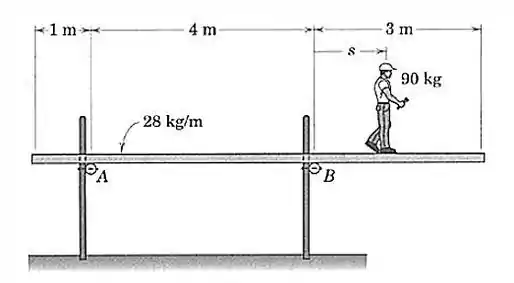
A plataforma uniforme, que tem uma massa por unidade de comprimento de , está simplesmente apoiada sobre barras de apoio em e em . Um trabalhador de construção civil com sai do ponto e anda para a direita. Em que posição o momento combinado do peso do homem e da plataforma será zero em relação ao ponto ?
Passo 1
Para resolver esta questão, vamos começar achando a força peso da plataforma e o seu ponto de aplicação. Repare que a placa tem de comprimento e foi dito no enunciado que ela possui por metro.
Então, a massa da plataforma () será de:
Vamos considerar a gravidade igual a , então o peso da plataforma () será:
E onde esta força está aplicada? Foi dito no enunciado que a plataforma é uniforme, então a força está localizada no seu centro de gravidade, que neste caso é na metade do seu comprimento:
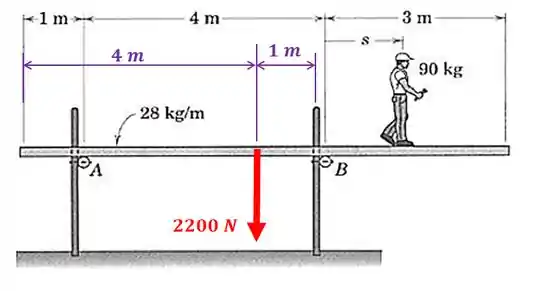
Passo 2
Agora vamos achar o peso do homem () que possui :
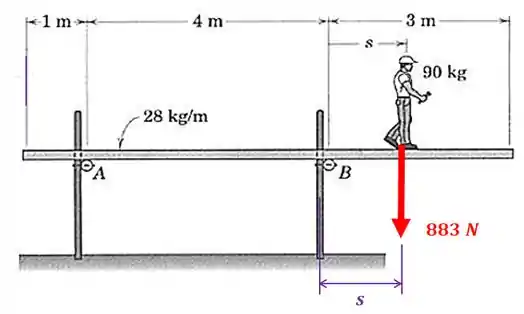
Passo 3
Vamos calcular o momento de cada uma dessas forças que achamos com relação ao ponto . Vamos começar pelo peso da plataforma:
Como esta força tende a girar no sentido anti-horário em torno do ponto , o momento que ela produzir será positivo, de acordo com a nossa convenção de sinais.
E o peso do homem? Nós não sabemos exatamente a distância que a força está do ponto , mas vamos chamar essa distância de :
Como esta força tende a girar no sentido horário, pela regra da mão direita seu polegar aponta para dentro da tela. Então, pela nossa convenção este momento será negativo:
Passo 4
A questão quer que o momento em torno do ponto seja zero, não é mesmo?
Mas sabemos que o momento em é igual a soma dos momentos produzidos com relação a este mesmo ponto por cada uma das nossas forças, então: