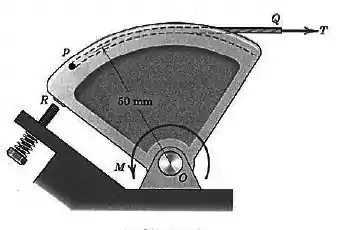
O componente de controle do acelerador pivota livremente em Se uma mola de torção interna exerce um momento de retorno sobre o componente, quando ele está na posição mostrada, determine, para a finalidade de projeto, a força trativa necessária no cabo do acelerador para que o momento resultante em torno de seja zero. Observe que quando é zero, o componente se apóia no parafuso do ajuste da marcha lenta em

Essa questão é mais fácil do que parece: Basta que a gente interprete corretamente o problema.

O que sabemos? Sabemos que em existe um momento aplicado.

E o que queremos? Queremos que o momento total seja nulo, ou seja:

E o que faremos pra que isso corra? Aplicaremos uma força , distante de , que gere um torque de sentido contrário.

É importante você perceber pela figura do problema que essa força é tangencial ao componente de controle. Isso é muito bom pois isso significa que não precisamos decompor a força.