Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.10 - Ex. 80

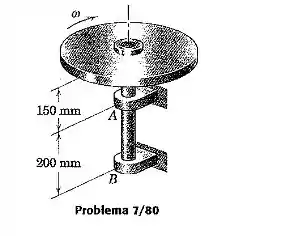
O disco circular de 6 kg e o eixo associado giram a uma velocidade angular constante ω = 10000   r p m . Se o centro de massa do disco está deslocado do centro em 0,05 mm, determine o módulo das forças horizontais A e B suportados pelos mancais em razão do desbalanceamento rotacional.

Passo 1

Vamos admitir que o eixo que corta o centro do disco é o eixo z assim nós teremos as seguintes componentes para velocidade angular ( ω ⃑ ) , ω ⃑ = ω z k ^

ω z = 10000   r p m = 10000 2 π 60 = 1047 r a d s

As equações 7/23 se reduzem para:

∑ M x = I y z ω z 2

Passo 2

O fato de o centro de massa do disco estar deslocado de 0,05 mm implicara que I y z ≠ 0 . Logo I y z utilizando o teorema dos eixos paralelos será I y z = 0 - x y m =

= - 0.15 50.10 - 6 6 = - 45.10 - 6 k g . m 2

∑ M x = - - 45.10 - 6 . 1047 = 0.047   k g . m 2 s

Devido a esse giro nós teremos um torque na direção de y ocasionado por uma força que chamaremos de B.

Onde ∑ M x = B . r e r = 200 m m = 0.2   m substituindo ∑ M x .

∑ M x = 0.047 = B . 0.2

B = 0.2   N

Passo 3

Agora se trocarmos os eixos de referência e colocarmos no eixo central de giro nós teremos I y z ' = 0 assim ∑ M x ' = 0 .

Onde ∑ M x = 0,35 B - 0,15 A = 0

A = 0.35 B 0.15 = 0.35 0.2 0.15 = 0,55   N

Resposta

B = 0.2   N

A = 0,55   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tábua de 25 kg está suspensa pelas cordas em C e D. Se essas cordas estão submetidas a forças constantes de 150 N e 225 N, respectivamente, determine a aceleração inicial do centro da tábua e sua ac
A bobina tem uma massa de 100 kg e um raio de giração k G = 0,3m . Se os coeficientes de atrito cinético e estático em A são μ s = 0,2 e μ k = 0,15 , respectivamente, determine a aceleração angular da
O disco semicircular tendo uma massa de 10 kg está girando a ω = 4r a d / s no instante θ = 60 ° . Se o coeficiente de atrito estático em A é μ s = 0,5 , determine se o disco desliza neste instante.
O rolo de grama tem uma massa de 80 kg e um raio de giração k G = 0,175m . Se ele for empurrado para frente com uma força de 200 N quando o punho está a 45°, determine sua aceleração angular. Os coefi
O foguete consiste de uma seção principal A tendo uma massa de 10 Mg e centro de massa em G A . Os dois foguetes auxiliares idênticos B e C têm cada um uma massa de 2 Mg com centros de massa em G B e