Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.5 - Ex. 101

101. Determine a frequência natural f n do pêndulo invertido. Assuma pequenas oscilações e indique quaisquer restrições sobre a sua solução.

v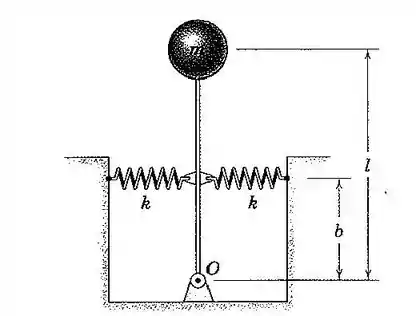

Passo 1

Bom, primeiro vamos montar o diagrama de corpo livre da esfera:

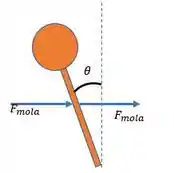
Vamos considerar o alongamento (ou compressão) inicial como sendo δ .

Passo 2

Agora, a gente vai montar a relação de energia total E T do sistema:

E T = V + T

Onde V é a energia cinética e T a energia potencial

Para V , temos:

1 2 m g ( l θ ˙ ) 2

Lembrando que v = ω r e ω = θ ˙ , e neste caso, r = l .

Agora, para T , temos a energia potencial gravitacional e a elástica.

Para a energia potencial temos:

- m g l ( 1 - cos ⁡ θ )

Já para a energia potencial elástica, teremos duas expressões, que diferenciarão em um fator, pois enquanto uma está comprimida, a outra está alongada.

+ 1 2 k ( δ + b ⋅ s e n θ ) + 1 2 k ( δ - b ⋅ s e n θ )

A expressão total nos da:

E T = 1 2 m g ( l θ ˙ ) 2 - m g l ( 1 - cos ⁡ θ ) + 1 2 k ( δ + b ⋅ s e n θ ) 2 + 1 2 k ( δ - b ⋅ s e n θ ) 2

Passo 3

Agora, vamos derivar a equação achada em relação ao tempo e assumir θ pequeno, pois ( s e n ( θ ) ≅ θ ) :

d d t E T = 0   ( C o n s t a n t e )

d d t 1 2 m g ( l θ ˙ ) 2 = m g l 2 θ ˙ θ ¨

d d t - m g l ( 1 - cos ⁡ θ ) = - m g l s e n ( θ ) θ ˙

d d t 1 2 k ( δ + b ⋅ s e n θ ) 2 = d d t 1 2 k ( ( δ ) 2 + 2 b ⋅ s e n θ + b ⋅ s e n θ 2

d d t 1 2 k ( δ + b ⋅ s e n θ ) 2 = 1 2 k ( 0 + 2 b ⋅ cos ⁡ θ θ ˙ + 2 b ⋅ s e n θ ⋅ b ⋅ cos ⁡ θ θ ˙ )

d d t 1 2 k ( δ - b ⋅ s e n θ ) 2 = d d t 1 2 k ( ( δ ) 2 - 2 b ⋅ s e n θ + b ⋅ s e n θ 2

d d t 1 2 k ( δ + b ⋅ s e n θ ) 2 = 1 2 k ( 0 - 2 b ⋅ cos ⁡ θ θ ˙ + 2 b ⋅ s e n θ ⋅ b ⋅ cos ⁡ θ θ ˙ )

Juntando tudo isso, temos:

m g l 2 θ ˙ θ ¨ - m g l ⋅ s e n θ θ ˙ + k b 2 ⋅ s e n θ ⋅ cos ⁡ θ θ ˙ + k b 2 ⋅ s e n θ ⋅ cos ⁡ θ θ ˙ =

m g l 2 θ ˙ θ ¨ - m g l θ θ ˙ + 2 k b 2 ⋅ θ ⋅ cos ⁡ θ θ ˙ = 0

Podemos observar que os termos k b ⋅ cos ⁡ θ θ ˙ e - k b ⋅ cos ⁡ θ θ ˙ se cancelam

Vamos dar uma arrumada na equação, simplificando e juntando os termos em comum:

m g l 2 θ ¨ + θ 2 k b 2 ⋅ cos ⁡ θ - m g l = 0

Mas, para θ bem pequeno, c o s ⁡ ( θ ) ≅ 1

m g l 2 θ ¨ + θ 2 k b 2 ⋅ 1 - m g l = 0

Deixando agora θ ¨ sozinho:

θ ¨ + θ 2 k b 2 - m g l m g l 2 = 0

Passo 4

Com isso, vamos achar o a frequência f n do sistema.

Sabemos que a fórmula genérica de um sistema massa-mola é dada por:

x ¨ + k m x = 0

Podemos ver que na equação que a gente achou:

k m = 2 k b - m g l m g l 2

E onde vamos usar isso? Bom! Para achar a frequência, primeiro temos que achar a frequência de ressonância pela fórmula:

ω n = 2 k b 2 - m g l m g l 2

Passo 5

Agora, para achar o a frequência, vamos usar a fórmula:

f n = ω n 2 π

f n = 1 2 π 2 k b 2 - m g l m g l 2

f n = 1 2 π 2 k b 2 m l 2 - g l   ( H z )

Porém, devemos prestar atenção nas condições da raiz:

2 k b 2 m l 2 - g l > 0

2 k b 2 m l 2 > g l

k > m g l 2 b 2

Resposta

A frequência natural f n do pêndulo invertido é:

f n = 1 2 π 2 k b 2 m l 2 - g l   ( H z )

Para:

k > m g l 2 b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um deslizador de 200g , sobre um trilho de ar, está preso a uma mola. O deslizador é puxado por 10c m e liberado. Com um cronômetro, um estudante constata que 10 oscilações levam 12,0s para ser comple
A posição de uma massa de 50g , em oscilação, é determinada pela relação x t =( 2,0c m )c o s ( 10 t - π / 4 ) , onde t está em s . Determine: a. A amplitude. b. O período. c. A constante elástica. d.
70. A amplitude de um oscilador com massa de 500g e período de 0,50s diminui em 2,0 % durante cada oscilação que ele efetua. a. Se a amplitude inicial for de 10c m , qual será a amplitude após 25 osci
O movimento de uma partícula é dado por x t = ( 25 c m )c o s ( 10 t ) , onde t está em s . Em que instante a energia cinética é duas vezes maior do que a energia potencial?
A Equação 14.25 estabelece que 1 2 k A 2 = 1 2 m v m á x 2 á . O que isso significa? Escreva algumas linhas explicando como se deve interpretar esta equação