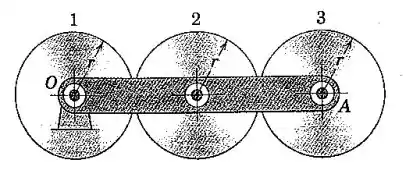
As três engrenagens 1, 2 e 3 de raios idênticos estão montadas no braço rotativo como indicado. (Os dentes de engrenagem estão omitidos no desenho). O braço AO gira no sentido horário em torno de O na taxa angular de 4 rad/s, enquanto a engrenagem 1 gira independentemente no sentido anti-horário na taxa de 8 rad/s. Determine a velocidade angular da engrenagem 3.

Bom pessoal, vamos começar fazendo um esboço da figura com os vetores velocidade:

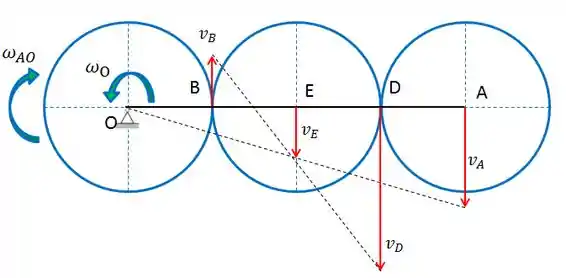
Beleza! Vamos calcular as velocidades dos centros das engrenagens a partir do braço rotativo AO:

Agora, vamos calcular as velocidades dos pontos de contato entre as engrenagens, chamados de B e D.

O ponto B pertence à engrenagem O. Portanto, o braço rotativo AO não tem influência na sua rotação. Somente vai ter influência a velocidade angular da própria engrenagem O. Então, para o ponto B vale a relação:

Para calcular a velocidade do ponto D, vamos fazer uma relação de triângulos mostrados na figura. Como possuem mesmo módulo, então a reta que passa pela ponta de seus vetores corta AO no centro, isto é, em .

Agora, basta usar o conceito de velocidade relativa entre os pontos D e A para descobrir a velocidade angular da última engrenagem: