Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 1
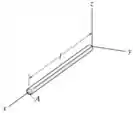
Determine o momento de inércia para a barra fina. A densidade da barra e a área de seção transversal são constante. Expresse o resultado em termos da massa total da barra.
Passo 1
Para a resolução desse exercício podemos considerar um da barra no eixo . Após isso, vamos aplicar a fórmula do momento de inércia. Com isso,
Passo 2
Sabemos que a massa pode ser calculada por , onde V é o volume. Então,
Passo 3
Substituindo a massa encontrada no Passo 2 no Passo 1, teremos
Resposta
Exercícios de Livros Relacionados
O reboque com sua carga tem uma massa de 150 kg e um centro de massa em G. Se ele é submetido a uma força horizontal P = 600 N, determine a aceleração do reboque e a força normal sobre o par de rodas
A empilhadeira de 1 Mg é usada para levantar a caixa de 750 kg com uma aceleração constante de 2 m/s². Determine a reação exercida pelo solo sobre o par de rodas em A e em B. Os centros de massa para
Determine a maior aceleração com a qual a empilhadeira de 1 Mg pode levantar a caixa de 750 kg, sem fazer com que as rodas em B deixem o solo. Os centros de massa para a empilhadeira e a caixa estão l
A motoesqui tem uma massa de 125 kg, centrada em G 1 , enquanto o motorista tem uma massa de 75 kg, centrada em G 2 . Se a aceleração é a = 6 m/s², determine a altura máxima h de G 2 do motorista, tal
A motoesqui tem uma massa de 125 kg, centrada em G 1 , enquanto o motorista tem uma massa de 75 kg, centrada em G 2 . Se h = 0,9 m, determine a aceleração permissível máxima da motoesqui a de maneira