Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 12

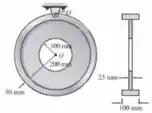
Determine o momento de inércia da montagem em relação a um eixo que é perpendicular à página e passa pelo ponto O . O material tem um peso específico de γ = 15KN/m3.

Passo 1

Para esse exercício, utilizaremos a fórmula dos eixos paralelos. Para tal, precisaremos do I G . Sabemos que I G = 1 2 ρ π x 2 d y x 2 e, pela figura do enunciado, temos dois anéis, sendo o primeiro deles mais externo e o segundo deles mais interno. Para o cálculo do momento de inércia vamos ter que considera-los indepentes. Então,

I G = 1 2 15000 π 0,25 2 0,1 0,25 2 - 1 2 1500 π 0,2 2 0,1 0,2 2 + 1 2 15000 π 0,2 2 0,025 0,2 2 - 1 2 15000 π 0,1 2 0,025 0,1 2

Resolvendo a expressão acima, vamos ficar com I G = 0,632 kg.m2

Passo 2

Agora que descobrimos o valor de I G , podemos calcular I O . Então,

I O = I G + m d 2

m = 15000 π 0,2 2 - 0,1 2 0,025 + 15000 π 0,025 0,1 = 153,15   m

Então,

I O = 0,632 + 153,15 0,25 2 = 10,204   k g . m 2

Resposta

I O = 10,204   k g . m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As quatro pás do ventilador têm uma massa total de 2 kg e momento e inércia I 0 = 0,18 kg.m² em relação a um eixo passando pelo centro do ventilador O. Se o ventilador é submetido a um momento M = 3 1
Se o motor no Problema 17.60 é desengatado do eixo assim que o volante está girando a 15 rad/s, de maneira que M = 0, determine quanto tempo vai levar antes que a resultante da força de atrito do manc
Um cabo é desenrolado de uma bobina apoiada em pequenos roletes em A e B exercendo uma força T = 300 N no cabo na direção mostrada. Calcule o tempo necessário para desenrolar da bobina 5 m de cabo se
O pêndulo consiste de uma esfera de 15 kg e uma barra fina de 5 kg. Calcule a reação no pino O logo após a corda AB ser cortada.
Os passageiros, a gôndola e sua estrutura de balanço têm uma massa total 50 Mg, um centro de massa em G e um raio de giração k B = 3,5 m. Adicionalmente, o bloco de aço de 3 Mg em A pode ser considera