Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 114
114. O motor elétrico possui uma massa total de e é apoiado pelos suportes de montagem e presos a plataforma giratória. A armadura do motor possui uma massa de e um raio de giração de e gira no sentido anti-horário a uma velocidade de , quando visualizada de para . A plataforma gira em torno de seu eixo vertical à taxa constante de no sentido mostrado. Determine as componentes verticais das forças suportadas pelos suportes de montagem em e .
Passo 1
Primeiramente, vamos fazer o esboço das forças, momentos dentre outras grandezas como precessão e giro, que estão atuando no nosso sistema de análise, considerando motor elétrico e armadura:
Primeiro o desenho do motor:
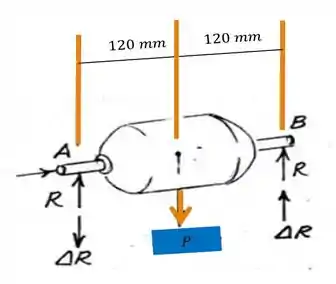
Segundo, o desenho da armadura:
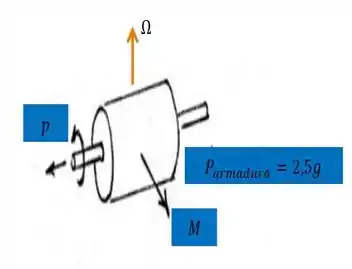
E em seguida, não podemos nos esquecer que a questão já nos fornce dois elementos que serão de extrema importância em nossa análise, a velocidade de giro , de e a precessão de . Como essas velocidades estão em , vamos multiplica-las por para convertê-las para :
Agora, vamos determinar aquela reação , no esboço que fizemos do motor elétrico. Para isso façamos o somatório das forças na direção igual a zero:
Onde é o peso do motor elétrico, que tem massa de :
Passo 2
E como podemos ver na segunda figura que esboçamos, a da armadura, temos a presença do momento , o que nos leva ao fato de que não podemos esquecer que ele está relacionado ao momento de inércia e à precessão pela seguinte fórmula, considerando é claro que eles estão em direções ortogonais, de modo que nem precisamos fazer o produto vetorial, uma vez que o seno do ângulo entre elas, de , é igual a :
Olha só que beleza. A questão já nos forneceu que o raio de giração é igual a . Podemos reescrever a fórmula de então, como:
E como sabemos os valores numéricos:
Bora tratar de substituir isso na fórmula, pois tá na cara dado que o momento que iremos obter é dado por:
Se você perceber, trata-se de um binário que está localizado a da origem no nosso centro de análise, que é onde está o centro de gravidade, por isso a multiplição por . Voltando ao que interesssa:
Passo 3
Por fim, como podemos ver na imagem que já temos, basta observar que uma força de reação é dada pela soma de com , enquanto a outra é dada pela subtração. Chamaremos essa forças de e :