Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas fundamentais - Ex. 11
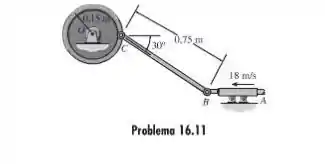
11. Se a barra AB desliza ao longo da ranhura horizontal com uma velocidade de 18 m/s, determine a velocidade angular da barra de ligação BC no instante mostrado.
Passo 1
Para encontrar a velocidade angular da barra de ligação, basta aplicarmos a equação da velocidade relativa entre os pontos B e C:
A partir daí, obtemos que:
Resposta
Exercícios de Livros Relacionados
9. Determine a velocidade angular da bobina. O cabo se enrola em torno do núcleo interno e a bobina não desliza na plataforma P.
7. Se o rolete A se desloca para a direita com uma velocidade constante v A = 3m / s , determine a velocidade angular da barra de ligação e a velocidade do rolete B no instante θ = 30 ° .
34. Se o eixo e a placa giram com uma velocidade angular constante ω = 14 r a d s , determine a velocidade e aceleração no ponto C localizado no canto da placa no instante mostrado. Expresse o resulta
40. O disco A rola sem deslizar sobre a superfície do cilindro fixo B. Determine a velocidade angular de A se seu centro C tem uma velocidade v C = 5 m s . Quantas revoluções A realizará em torno de s
33. Se a barra parte do repouso na posição mostrada e um motor a aciona por um curto período com uma aceleração angular a = 1,5 e t r a d s 2 , onde t é dado em segundos, determine a intensidade da ve