Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 11
11. As componentes do estado plano de deformação no ponto sobre a chave de porca são , e ). Use as equações de transformação da deformação para determinar as deformações principais no plano e a deformação por cisalhamento máxima no plano e a deformação normal média. Em cada caso, especifique a orientação do elemento e mostre como as deformações distorcem o elemento no plano .
Passo 1
Falaa! A gente precisa das deformações nos planos principais e no de cisalhamento máximo. Basicamente, vamos usar as fórmulinhas para essas grandezas e fazer um desenho com os nossos resultados, mostrando como o elemento está deformado.
Primeiro, calcularemos as deformações principais no plano:
Trocando os valores numéricos na fórmula:
Passo 2
Calculando, em seguida, a tangente de :
Como :
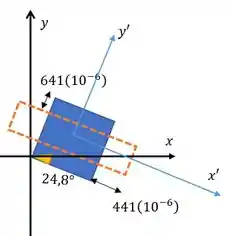
Essa é a direção de . E o outro ângulo é dado por:
Essa é a direção de .
Passo 3
A gente tem as deformações e a orientação dos eixos principais. Mas que deformação está em cada eixo. está relacionada ao eixo de ou ? Não sabemos! Por isso, precisamos calcular a deformação na orientação de , para saber se é ou .
Calculando agora dado que sabemos o valor de :
E substituindo os valores numéricos pertinentes, chega-se à:
Logo, temos que
Nosso elemento deformado fica:
Passo 4
Depois, calcularemos a deformação por cisalhamento máxima no plano:
Trocando por valores numéricos:
Passo 5
Precisamos também da deformação normal média, né! Pois vamos trata de encontrá-la:
Que é igual a:
Passo 6
Por último, calculemos a tangente de :
Como :
E o outro ângulo , nós encontramos como:
Aqui o nosso elemento fica:
Repara que como é negativa, nas direções normais, nosso elemento encurtou.
Resposta
As deformações principais no plano são:
A deformação por cisalhamento máximo é:
E a deformação normal média:
