Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 110
110. Se a roda no caso (a) do problema é forçada a executar uma precessão em torno da vertical, por um acionamento mecânico na taxa constante de , determine o momento fletor na haste horizontal em . Na ausência de atrito, qual o torque é aplicado a luva em para manter esse movimento?
Passo 1
A questão diz que a roda do nosso problemaé forçada a executar uma precessão em torno da vertical. Vamos então fazer o esboço dos esforços presentes no nosso sistema.
Primeiro, para a haste que sustenta a roda:
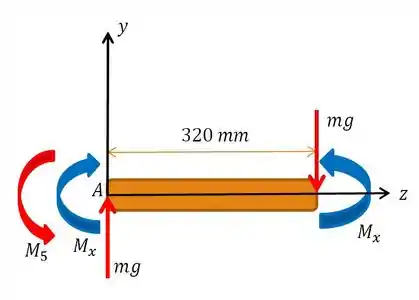
E depois, para não perder a viagem, bora fazer o esboço dos esforços presentes, considerando dessa vez a vista lateral da nossa roda, juntamente com o sentido do giro e da precessão . Vale lembrar, que o momento , o giro e precessão são todos ortogonais.
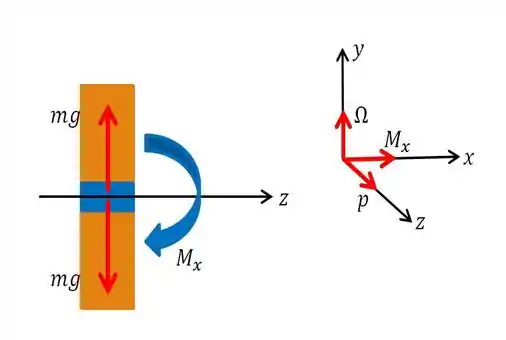
E olhando a figura, tem duas coisas que já podemos tirar logo de cara, que é:
O esforço da força peso, igual a:
E a precessão , igual a:
Passo 2
E como podemos ver na segunda figura que esboçamos temos a presença do momento, o que nos leva ao fato de que não podemos esquecer que ele está relacionado ao momento de inércia e à precessão pela seguinte fórmula, considerando é claro que eles estão em direções ortogonais, de modo que nem precisamos fazer o produto vetorial:
Olha só que beleza. A questão já nos forneceu que o raio de giração é igual a . Podemos reescrever a fórmula de então, como:
E como sabemos os valores numéricos:
Bora tratar de substituir na fórmula, pois tá na cara que é o momento que iremos obter:
Obtido o valor de , voltemos à seguinte imagem:
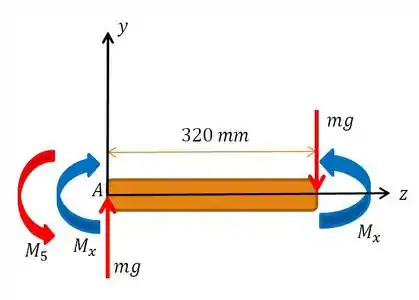
Tá na cara que o valor do momento fletor em , dado por , é obtido pela subtração dos momentos e :
Onde é obtido fazendo o somatório dos momentos na haste, como exposto abaixo:
Com isso, obtemos o valor do momento fletor em :
Passo 3
Em relação ao torque aplicado na ausência de atrito, temos que como a própria questão fala que não existe atrito, a precessão será uma constante, pelo qual a sua derivada temporal , que será obviamente igual a zero.
E qual é mesmo a fórmula que relaciona precessão e o momento . Acho que ela tem a seguinte cara:
Como , então tiramos que: