Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 228
As duas barras esbeltas, cada uma com uma massa de 4 kg, são articuladas em e . Se um impulso horizontal é aplicado à extremidade da barra inferior, por um intervalo de 0,1 s, durante o qual as barras ainda estão praticamente nas suas posições verticais de repouso, calcule a velocidade angular da barra superior imediatamente após o impulso.
Passo 1
O enunciado nos dá as seguintes informações:
Massa de cada barra: ;
Impulso horizontal: ;
Intervalo de tempo de aplicação do impulso: .
Nestas condições, devemos calcular a velocidade angular da barra superior imediatamente após o impulso.
Além disso, durante este intervalo de tempo, as barras ainda estão praticamente nas suas posições verticais de repouso, ou seja, trata-se de um deslocamento infinitesimal.
Vamos desenhar o diagrama de corpo livre e cinético das barras:
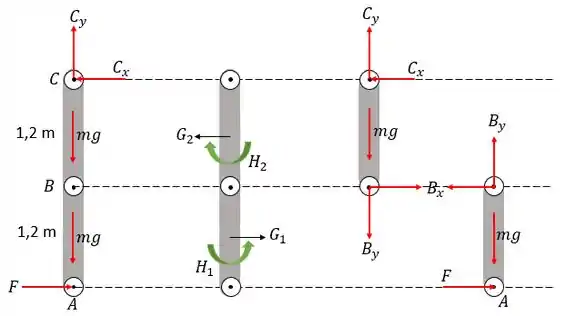
Passo 2
Primeiramente, vamos encontrar o momento de inercia da barra:
Sabemos que
Logo, neste caso, temos
Passo 3
Em seguida, vamos encontrar a velocidade angular da barra:
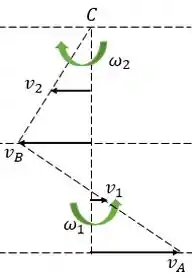
O enunciado pede o valor de . Sabemos que , portanto devemos encontrar o valor de .
Temos que
Analisando o sistema e utilizando o ponto como referência, temos que
Logo,
Agora, vamos analisar as barras individualmente.
Para a barra , temos
E
Passo 4
Agora vamos analisar as equações obtidas no passo anterior.
Resolvendo o sistema
Obtemos
Resolvendo o sistema
Obtemos
Combinando as duas equações obtidas, chegamos à
Logo,