Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 36
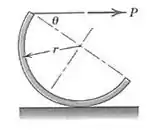
6/36) A casca semicil´ndrica de massa e raio é girada de um ângulo no qual a casca escorrega sobre asuperfície horizontal à medida que aumenta gradualmente . Que valor de permitirá que atinja ?
Passo 1
Então galera , seja o ponto de contato da casca semicilíndrica e o solo , e seja a distância entre o centro da semicircunferência e o centro de massa da casca semicilíndrica .
Com isso definido , aplicando as equações de equilíbrio que conhecemos , temos que :
Logo ,
Passo 2
Combinando as equações obtidas no passo anterior , achamos que :
Dessa forma ,
Sendo assim ,
Para , temos que :
Portanto ,
Resposta
Tranquilo pessoal? Então partiu resolver mais questões
Exercícios de Livros Relacionados
Os coeficientes de atrito são μ s = 0,4 e μ k = 0,3 entre todas as superfícies de contato. Determine a menor força P necessária para iniciar o movimento do bloco de 30 kg se o cabo AB ( a ) está ligad
Determine o intervalo de valores de P para o qual o equilíbrio do bloco mostrado na figura é mantido.
Considerando apenas valores de θ menores que 90°, determine o menor valor de θ solicitado para o qual o movimento do bloco para a direita é iminente quando ( a ) W = 340 N, ( b ) W = 450 N.
Os coeficientes de atrito entre o bloco e o trilho são μ s = 0,3 e μ k = 0,25 . Sabendo que θ = 65 ° , determine o menor valor da força P necessária ( a ) para iniciar o movimento do bloco sobre o tri
O bloco de 360 N está ligado à articulação AB e repousa sobre uma esteira em movimento. Sabendo que μ s = 0,25 e μ k = 0,2 determine a intensidade da força horizontal P que pode ser aplicada na esteir