Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas fundamentais - Ex. 4

Determine a aceleração máxima do caminhão sem fazer com que a montagem se desloque em relação ao caminhão. Além disso qual é a reação normal correspondente sobre as pernas A e B ? A mesa de 100   k g tem um centro de massa G e o coeficiente de atrito estático entre as pernas da mesa e o piso da carroceria do caminhão é μ s = 0,2 .

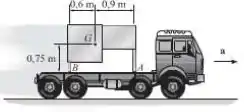
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O exercício nos pede a aceleração máxima do caminhão sem fazer com que a montagem se desloque em relação ao caminhão.

Ou seja, o movimento n pode vencer a força de atrito da montagem:

F A = μ s N A = 0,2 N A

F B = μ s N B = 0,2 N B

Vamos à análise horizontal:

→ + ∑ F x = m a G x

0,2 N A + 0,2 N B = 100 ( a )

Para a análise dinâmica das forças verticais, temos:

+ ↑ ∑ F y = m a G y

Sabemos que a aceleração do sistema no eixo y é nula, portanto:

N A + N B - 100 9,81 = 0

Passo 2

Para determinar a aceleração do sistema, podemos analisar o momento provocado pela aceleração:

∑ M G = 0

0,2 N A 0,75 + N A 0,9 + 0,2 N B 0,75 - N B ( 0,6 ) = 0

1,05 N A - 0,45 N B = 0

N A = 0,42857 N B

Substituindo na equação encontrada na análise vertical, temos:

0,42857 N B + N B - 100 9,81 = 0

N B = 686,7   N

N A = 0,42857 686,7

N A = 294,3   N

A aceleração será:

0,2 ( 294,3 ) + 0,2 ( 686,7 ) = 100 ( a )

a = 1,962   m / s 2

Resposta

N B = 686,7   N

N A = 294,3   N

a = 1,962   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A roda com raio de 100 mm possui uma massa de 3 kg e gira em torno de seu eixo y ' com uma velocidade angular p = 40 ⋅ πr a d / s no sentido indicado. Simultaneamente, o garfo gira em torno do eixo x
A placa retangular, com uma massa de 3 kg e uma pequena espessura uniforme, está soldada no ângulo de 45º ao eixos vertical, que gira com a velocidade angular de 20 ⋅ πr a d / s . Determine a quantida
Cada uma das duas hastes de massa m está soldada à face do disco que gira em torno do eixo vertical, com uma velocidade angular constante ω . Determine o momento fletor M que atua na base de uma das h
Calcule o momento fletor M na haste vertical em O para o conjunto do Prob. 7/78 devido a sua aceleração angular, quando o conjunto parte do repouso sob a ação de um torque de 64N ⋅ m aplicado à haste
Determine as forças normais sob os dois discos do Exemplo para a posição em que o plano da barra curva é vertical. Assuma que a barra curva está na parte superior do disco a e na parte inferior do dis