Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 116
116- Resolva o Problema , considerando que o cabo é substituído por um cabo preso no ponto e no gancho em .
Passo 1
Essa mudança vai fazer com que tenha somente um cabo agora fazendo com que tenha o seguinte diagrama de forças agora.
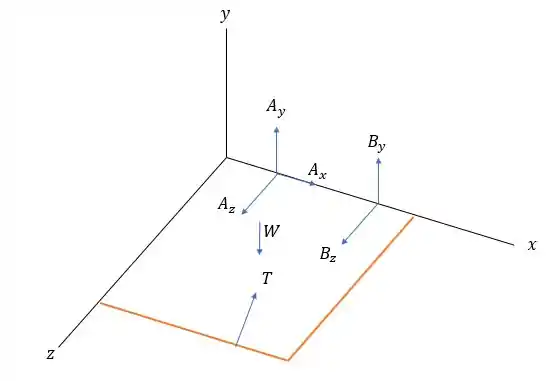
Como vimos a vetorização da força em na questão anterior poderemos escrever os determinantes da somatória dos momentos em da seguinte maneira:
O que nos dá:
Fazendo a somatória das componentes que tem temos:
E as reações em acharemos somando as componentes com e .
Logo a reação em será:
Passo 2
Agora fazendo a somatória das forças e igualando a zero nós teremos as forças em .
O que nos dará:
Logo a reação em será:
Resposta
Exercícios de Livros Relacionados
O poste rígido e as traves cruzadas do Prob. 2 / 105 estão mostrados novamente aqui. Determine as forças trativas T A E e T G F nos dois cabos de sustentação devidas à força trativa de 1,2k N no cabo
Uma porta homogênea de massa m , altura h e largura w está encostada em uma parede para ser pintada. Pequenas ripas de madeira estão colocadas sob as quinas A ,B e C . O atrito em C é desprezível, mas
Um letreiro retangular sobre uma loja tem uma massa de 100k g e seu centro de massa está no centro do retângulo. A sustentação contra a parede no ponto C pode ser considerada como uma rótula. Na extre
O painel retangular uniforme A B C D tem uma massa de 40k g e tem dobradiças entre seus vértices A e B e a superfície vertical rígida. Um arame ligando E a D mantém horizontais as bordas B C e A D . A
O plano vertical pelo qual passa o cabo de eletricidade gira de 30 ° no poste vertical O C . As forças trativas T 1 e T 2 valem ambas 950N . Para prevenir inclinação do poste com o passar do tempo, os