122. Um projétil que se desloca através da atmosfera com uma velocidade que faz um pequeno ângulo com seu eixo geométrico é submetido a uma força aerodinâmica resultante essencialmente no sentido oposto a conforme indicado. Se passa através de um ponto ligeiramente a frente do centro de massa , determine a expressão para a velocidade de giro mínima para a qual o projétil sera estabilizado pelo giro com . O momento de inércia em relação ao eixo de giro é e em relação a um eixo transversal através de é . Expresse o resultado como uma equação quadrática em e determine o valor mínimo de para o qual a expressão sob o radical é positivo.
Passo 1
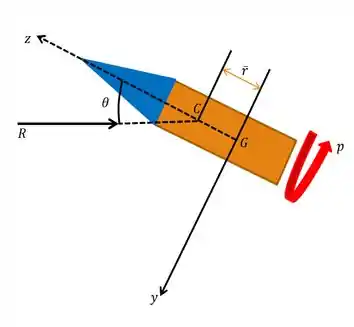
Primeiramente, vamos fazer o esboço do nosso sistema posicionando-o em um sistema de eixos coordenados:
Passo 2
Agora, vamos fazer o somatório das forças no eixo . Você deve estar se perguntando que eixo é esse que eu não estou vendo? Bem! O eixo está saindo para fora desse plano, de modo que ele vai ser dado por:
Só que como trata-se de uma precessão em regime estacionário, onde temos um ângulo constante e uma velocidade de giro constante, temos que pode ser escrito como:
E dado o fato de que a precessão está relacionada com a velocidade e o ângulo de giro, respectivamente e , e ao momento de inércia pela seguinte fórmula:
Existem alguma relações que podemos usar na fórmula anterior. São elas:
E substituindo essas relações, ficamos com:
Passo 3
Olha só que beleza! Obtemos no final do uma equação do segundo grau da forma , cujas raízes são dadas por:
Substituindos nessas conta os valores da equação que queremos, onde:
Obtemos nossas raízes iguais a:
Pronto! Chegamos na relação que queríamos, pois esse radical presente na última expressão que obtivemos precisa obrigatoriamente ser mais ou igual a zero:
E como a questão pede o valor mínimo de para o qual a expressão sob o radical é positivo, logo mínimo é dado por: