Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 72

Em um teste dos painéis solares para uma nava espacial, o modelo apresentado está girando em torno do eixo vertical na velocidade angular ω .   Se a massa por unidade de área do painel é ρ , escreva a expressão para a quantidadede movimento angular H o   do conjunto em relação a os eixos mostrados, em termos de θ . Determine também os valores máximos, mínimo e intermediário dos momentos de inércia em relação aos eixos atráves de O.

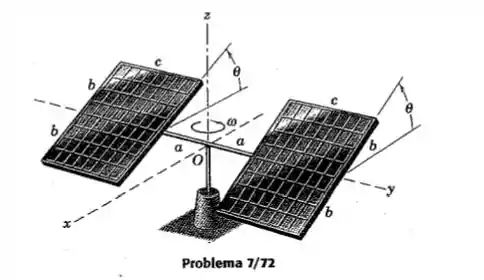
Passo 1

Podemos simplificar a configuração acima da seguinte forma:

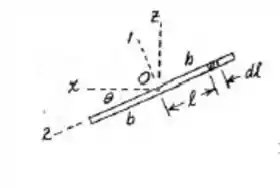
fazendo isso nós teremos que x = l c o s θ   e   z = l s i n ( θ )

Também teremos a velocidade angular com somente uma componente ω = ω k ^ .

Que simplifica a equação 7/11 da forma:

H o = - I x z ω i ^   - I y z ω j ^ + I z z ω k ^

Passo 2

Agora calculamos as componentes necessárias do tensor de inercia.

I x z = ∫ - x z d m = ∫ - x z ρ d A = ∫ - b b - l c o s θ l s e n θ 2 c ρ d l =  

= cos ⁡ θ s e n θ 2 c ρ ∫ - b b - l 2 d l = 2 3 ρ c b 3 s e n ( 2 θ )  

I y z   = ∫ - y z d m = 0 note que que esse problema é semelhante ao problema 7/70 só muda o eixo que está fixo.

Por fim I z z = 1 12 m L 2 + m d 2

L 2 = c 2 + 2 b c o s θ 2

Como ρ = m A nós teremos m = ρ A = 4 b c ρ

d = a + c 2

I z z = 1 12 4 b c ρ c 2 + 2 b c o s θ 2 + 4 b c ρ a + c 2 2

I z z = 4 b c ρ ( c 2 3 + b 2 3 cos 2 ⁡ θ + a 2 + a c )

Passo 3

Voltando agora em H o nós ficamos com.

H o = - 2 3 ρ c b 3 s e n 2 θ ω i ^ + 4 b c ρ ( c 2 3 + b 2 3 cos 2 ⁡ θ + a 2 + a c ) ω k ^  

Resposta

H o = - 2 3 ρ c b 3 s e n 2 θ ω i ^ + 4 b c ρ ( c 2 3 + b 2 3 cos 2 ⁡ θ + a 2 + a c ) ω k ^  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pêndulo consiste de uma esfera de 15 kg e uma barra fina de 5 kg. Calcule a reação no pino O logo após a corda AB ser cortada.
Os passageiros, a gôndola e sua estrutura de balanço têm uma massa total 50 Mg, um centro de massa em G e um raio de giração k B = 3,5 m. Adicionalmente, o bloco de aço de 3 Mg em A pode ser considera
Os passageiros, a gôndola e sua estrutura de balanço têm uma massa total 50 Mg, um centro de massa em G e um raio de giração k B = 3,5 m. Adicionalmente, o bloco de aço de 3 Mg em A pode ser considera
Um motor fornece um torque constante M = 2 N.m para o eixo de 50 mm de diâmetro O conectado ao centro do volante de 30 kg. O atrito resultante do mancal F, que o mancal exerce sobre o eixo, atua tange
O diagrama cinético representando o movimento rotacional geral de um corpo rígido em torno de um eixo fixo passando por O é mostrado na figura. Mostre que I G α pode ser eliminado deslocando os vetore