Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 66

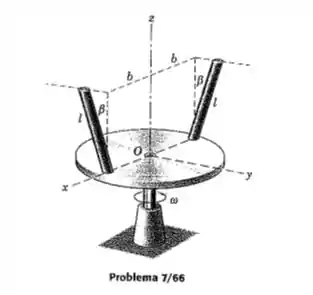
Cada uma das hastes esbeltas de comprimento l e massa m está soldada ao disco circular que gira em torno do eixo vertical z com uma velocidade angular ω . Cada haste faz um ângulo β com a vertical e está situada em um plano paralelo ao plano y-z. Determine uma expressão para a quantidade de movimento angular H o das duas hastes em relação a origem.

Passo 1

Primeiramente vamos analisar o comportamento do giro para esse problema. Pela regra da mão direita nós teremos somente uma componente da velocidade angular que será ω = ω k ^ e por consequência ω y = ω x = 0

Assim as equações 7/12 se reduzem em:

H x 0 = - I x z ω

H y 0 = - I y z ω

H z 0 = I z z ω

H o = - I x z ω i ^   - I y z ω j ^ + I z z ω k ^

Passo 2

Podemos considerar as hastes como barras finas, portanto quando formos calcular o momento de inercia em relação ao o eixo x-z e y-z será zero.

I x z = I y z = 0

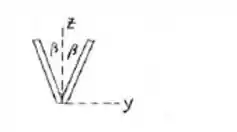
Para I z z nós podemos utilizara está configuração:

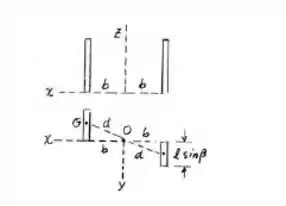
Iremos utilizar o teorema dos eixos paralelos para calcula-los, e também somando as duas contribuições das duas hastes

I z z = 2 I G + 2 m d 2

Sendo I G = 1 12 m l 2 e l = l s e n ( β )

E d 2 = b 2 + l 2 4 s e n 2 ( β )

I z z = 2 ( 1 12 m l s e n β 2 + m ( b 2 + l 2 4 s e n 2 β )

I z z = 2 m ( 1 3 l 2 s e n 2 β + b 2 )

Assim substituindo em H o

H o = 2 m 1 3 l 2 s e n 2 β + b 2 ω k ^

Resposta

H o = 2 m 1 3 l 2 s e n 2 β + b 2 ω k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A motoesqui tem uma massa de 125 kg, centrada em G 1 , enquanto o motorista tem uma massa de 75 kg, centrada em G 2 . Se a aceleração é a = 6 m/s², determine a altura máxima h de G 2 do motorista, tal
A motoesqui tem uma massa de 125 kg, centrada em G 1 , enquanto o motorista tem uma massa de 75 kg, centrada em G 2 . Se h = 0,9 m, determine a aceleração permissível máxima da motoesqui a de maneira
O avião a jato é propelido por quatro motores para aumentar sua velocidade uniformemente do repouso até 100 m/s em uma distância de 500 m. Determine o empuxo T desenvolvido por todos os motores e a re
Uma placa uniforme tem uma massa de 25 kg. O membro AB está submetido a um momento binário M = 15 N.m e tem uma velocidade angular no sentido horário de 2 rad/s no instante θ = 30 ° . Determine a forç
A caixa uniforme de 50 kg repousa sobre a plataforma para a qual o coeficiente de atrito estático é μ s = 0,5 . Se no instante θ = 30 ° os membros-apoio têm uma velocidade angular ω = 1 rad/s e aceler